Übersicht - Zahlengruppen

• \N = \{1,2,...\}$\N = \{1,2,...\}$: natürliche Zahlen
  • \N_0 = \{0, 1,2,...\}$\N_0 = \{0, 1,2,...\}$: natürliche Zahlen mit 0
• \Z = \{..., -2, -1, 0, 1,2,...\}$\Z = \{..., -2, -1, 0, 1,2,...\}$: ganze Zahlen
• \mathbb{Q}$\mathbb{Q}$: rationale Zahlen (e.g. Bruchzahlen)
• \mathbb{R}$\mathbb{R}$: reele Zahlen (irrationale Zahlen)
• \mathbb{C}$\mathbb{C}$: komplexe Zahlen
  • Zahlen vom Typ: z = a + bi$z = a + bi$
    • re(z) = a$re(z) = a$ (Realteil, a \in \R$a \in \R$) und im(z) = b$im(z) = b$ (Imaginärteil, b \in \R$b \in \R$)
    • i = \sqrt{-1}, i^2=-1$i = \sqrt{-1}, i^2=-1$
      • x^2 + a = 0$x^2 + a = 0$
      • x^2 = -a$x^2 = -a$
        • x_{1,2} = \pm \sqrt{-a} = \pm \sqrt{-1} \sqrt{a} = \pm i \sqrt{a}$x_{1,2} = \pm \sqrt{-a} = \pm \sqrt{-1} \sqrt{a} = \pm i \sqrt{a}$

Komplexe Zahlen

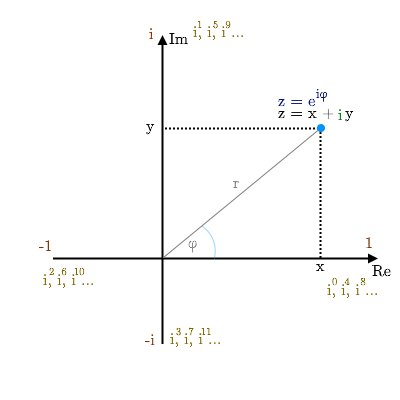
• komplexe Zahl: z = a + bi$z = a + bi$
• konjugiert komplexe Zahl: \overline z = a - bi$\overline z = a - bi$ (gespiegelt an der reelen Achse)
• Absolutbetrag / Länge / Norm: |z| = \sqrt{a^2 + b^2} = \sqrt{z * \overline z}$|z| = \sqrt{a^2 + b^2} = \sqrt{z * \overline z}$
• Dreiecksungleichung: |z + w| \leq |z| + |w|$|z + w| \leq |z| + |w|$

Operationen

• Addition und Subtraktion:
  • karthesische Darstellung verwenden
  • z_1 \pm z_2 = (a_1 \pm a_2) + i * (b_1 \pm b_2)$z_1 \pm z_2 = (a_1 \pm a_2) + i * (b_1 \pm b_2)$
    • z.B. z_1 = 2 - 3i, z_2 = 4 + 5i$z_1 = 2 - 3i, z_2 = 4 + 5i$
      • z_1 + z_2 = (2 + 4) + i * (-3 + 5) = 6 + 2i$z_1 + z_2 = (2 + 4) + i * (-3 + 5) = 6 + 2i$
      • z_1 - z_2 = (2 - 4) + i * (-3 - 5) = -2 -8i$z_1 - z_2 = (2 - 4) + i * (-3 - 5) = -2 -8i$
      • \overline{z_1} = 2 + 3i$\overline{z_1} = 2 + 3i$
      • \overline{z_2} = 4 - 5i$\overline{z_2} = 4 - 5i$
      • |z_1| = \sqrt{2^2 + (-3)^2} = \sqrt{4 + 9} = \sqrt{13}$|z_1| = \sqrt{2^2 + (-3)^2} = \sqrt{4 + 9} = \sqrt{13}$
      • |z_2| = \sqrt{4^2 + 5^2} = \sqrt{16 + 25} = \sqrt{41}$|z_2| = \sqrt{4^2 + 5^2} = \sqrt{16 + 25} = \sqrt{41}$
• Multiplikation:
  • Polardarstellung verwenden
    • Längen multiplizieren sich
    • Winkel addieren sich
    • z_1* z_2 = r_1 * r_2 (cos(\varphi_1 + \varphi_2) + i * sin(\varphi_1 + \varphi_2)) = r_1*r_2*e^{i*(\varphi_1 + \varphi_2)}$z_1* z_2 = r_1 * r_2 (cos(\varphi_1 + \varphi_2) + i * sin(\varphi_1 + \varphi_2)) = r_1*r_2*e^{i*(\varphi_1 + \varphi_2)}$
  • in Koordinatendarstellung: z_1* z_2 = (a_1 * a_2 - b_1 * b_2) + i * (a_1 * b_2 + a_2 * b_ 1)$z_1* z_2 = (a_1 * a_2 - b_1 * b_2) + i * (a_1 * b_2 + a_2 * b_ 1)$
    • z.B. z_1 = 2 - 3i, z_2 = 4 + 5i$z_1 = 2 - 3i, z_2 = 4 + 5i$
      • z_1 * z_2 = (2 * 4 - (-3) * 5) + i * (2 * 5 + 4 * (-3)) = 23 - 2i$z_1 * z_2 = (2 * 4 - (-3) * 5) + i * (2 * 5 + 4 * (-3)) = 23 - 2i$
• Division:
  • \frac{z_1}{z_2} = \frac{a_1*a_2+b_1*b_2}{a_2^2+b_2^2} + i * \frac{a_2*b_1+a_1*b_2}{a_2^2+b_2^2}$\frac{z_1}{z_2} = \frac{a_1*a_2+b_1*b_2}{a_2^2+b_2^2} + i * \frac{a_2*b_1+a_1*b_2}{a_2^2+b_2^2}$
  • |\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$|\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$
  • \overline{(\frac{z_1}{z_2})} = \frac{\overline{z_1}}{\overline{z_2}}$\overline{(\frac{z_1}{z_2})} = \frac{\overline{z_1}}{\overline{z_2}}$
• Sonderregeln:
  • \overline{z_1 \pm z_2} = \overline{z_1} \pm \overline{z_2}$\overline{z_1 \pm z_2} = \overline{z_1} \pm \overline{z_2}$
  • \overline{z_1 * z_2} = \overline{z_1} * \overline{z_2}$\overline{z_1 * z_2} = \overline{z_1} * \overline{z_2}$
  • |z_1 * z_2| = |z_1| * |z_2|$|z_1 * z_2| = |z_1| * |z_2|$
  • z * \overline z = |z|^2$z * \overline z = |z|^2$
    • z.B. z = 1 + i, \overline z = 1 - i \to |z| = \sqrt{1^2+1^2} = \sqrt2$z = 1 + i, \overline z = 1 - i \to |z| = \sqrt{1^2+1^2} = \sqrt2$
• Gleichheit zweier komplexen Zahlen:
  • a + ib = c + id \Leftrightarrow a = c \;\land\; b = d$a + ib = c + id \Leftrightarrow a = c \;\land\; b = d$
• Invertieren einer komplexen Zahl:
  • Multiplizieren mit dem konjugiert Komplexen des Nenners
    • z.B. \frac{1}{2+3i}*\frac{2-3i}{2-3i} = \frac{2-3i}{(2+3i)(2-3i)} = \frac{2+3i}{13} = \frac{2}{13} - \frac{3}{13}i$\frac{1}{2+3i}*\frac{2-3i}{2-3i} = \frac{2-3i}{(2+3i)(2-3i)} = \frac{2+3i}{13} = \frac{2}{13} - \frac{3}{13}i$

Potenzen von i

• i^1 = i$i^1 = i$
• i^2 = -1$i^2 = -1$
• i^3 = -i$i^3 = -i$
• i^4 = 1$i^4 = 1$

Darstellungsformen von komplexen Zahlen

• karthesisches Koordinatensystem:
  • z = a + bi$z = a + bi$
    • re(z) = a$re(z) = a$ (Realteil, a \in \R$a \in \R$)
    • im(z) = b$im(z) = b$ (Imaginärteil, b \in \R$b \in \R$)
• Polarkoordinaten:
  • Eulersche Identität: z = e^{i * \varphi} = \cos(\varphi) + i * \sin(\varphi)$z = e^{i * \varphi} = \cos(\varphi) + i * \sin(\varphi)$
  • Polardarstellung mit r = |z|, r > 0$r = |z|, r > 0$: z = r * e^{i * \varphi} = r * (\cos(\varphi) + i * \sin(\varphi))$z = r * e^{i * \varphi} = r * (\cos(\varphi) + i * \sin(\varphi))$

Umrechnungsformeln

• Karthesisches Koordinatensystem \to$\to$ Polardarstellung:
  • gegeben: a + ib$a + ib$
    • r = \sqrt{a^2 + b^2}$r = \sqrt{a^2 + b^2}$
    • \varphi = \arccos(\frac{a}{r})$\varphi = \arccos(\frac{a}{r})$ für b \geq 0$b \geq 0$
    • \varphi = - \arccos(\frac{a}{r})$\varphi = - \arccos(\frac{a}{r})$ für b < 0$b < 0$
• Polardarstellung \to$\to$ Karthesisches Koordinatensystem
  • gegeben: (r, \varphi)$(r, \varphi)$
    • a = r * \cos \varphi$a = r * \cos \varphi$
    • b = r * \sin \varphi$b = r * \sin \varphi$

Additionstheoreme

• -\sin(\varphi) = \sin(-\varphi)$-\sin(\varphi) = \sin(-\varphi)$
• \cos(-\varphi) = \cos(\varphi)$\cos(-\varphi) = \cos(\varphi)$
• \cos(\varphi_1 + \varphi_2) = \cos(\varphi_1) * \cos(\varphi_2) - \sin(\varphi_1) * \sin(\varphi_2)$\cos(\varphi_1 + \varphi_2) = \cos(\varphi_1) * \cos(\varphi_2) - \sin(\varphi_1) * \sin(\varphi_2)$
• \sin(\varphi_1 + \varphi_2) = \sin(\varphi_1) * \cos(\varphi_2) + \cos(\varphi_1) * \sin(\varphi_2)$\sin(\varphi_1 + \varphi_2) = \sin(\varphi_1) * \cos(\varphi_2) + \cos(\varphi_1) * \sin(\varphi_2)$
• e^{i * \varphi_1} * e^{i * \varphi_2} = e^{i * (\varphi_1 + \varphi_2)}$e^{i * \varphi_1} * e^{i * \varphi_2} = e^{i * (\varphi_1 + \varphi_2)}$

Gleichungen mit komplexen Zahlen

• Ausklammern und Nullprodukt
  • z.B. z^3 + z = 0$z^3 + z = 0$
    • z(z^2+1)=0 \to z_1 = 0$z(z^2+1)=0 \to z_1 = 0$
    • z^2+1=0 \to z^2=-1 \to z_{2,3} = \pm i$z^2+1=0 \to z^2=-1 \to z_{2,3} = \pm i$
    • \mathbb{L}=\{0, -i, i\}$\mathbb{L}=\{0, -i, i\}$
• mit z$z$ konjugiert:
  • z.B. (z - 1)^2 = (z + 1)^2 + z * \overline z$(z - 1)^2 = (z + 1)^2 + z * \overline z$
    • z^2 -2zi + i^2 = z^2 + 2zi + i^2 + z * \overline z$z^2 -2zi + i^2 = z^2 + 2zi + i^2 + z * \overline z$
    • -2zi = 2zi + z * \overline z$-2zi = 2zi + z * \overline z$
    • 0 = 4zi + z * \overline z$0 = 4zi + z * \overline z$
    • 0 = z(4i + \overline z)$0 = z(4i + \overline z)$
      • z_1 = 0$z_1 = 0$
      • 4i + \overline z = 0 \to \overline z = -4i \to z_2 = 4i$4i + \overline z = 0 \to \overline z = -4i \to z_2 = 4i$
• quadratische Gleichung:
  • z.B. z^2 + 2z + 3 = 0$z^2 + 2z + 3 = 0$
    • z_{1,2} = -1 \pm \sqrt{-2} = -1 \pm i * \sqrt 2$z_{1,2} = -1 \pm \sqrt{-2} = -1 \pm i * \sqrt 2$
      • z_1 = -1 + i * \sqrt 2$z_1 = -1 + i * \sqrt 2$
      • z_2 = -1 - i * \sqrt 2$z_2 = -1 - i * \sqrt 2$
  • z.B. z^2 + 2z - i = 0$z^2 + 2z - i = 0$
    • z_{1,2} = -1 \pm \sqrt{1+i}$z_{1,2} = -1 \pm \sqrt{1+i}$
      • u^2 = 1+i$u^2 = 1+i$ mit u: 22,5°$u: 22,5°$ (45° / 2$45° / 2$, da |1+i| = \sqrt 2$|1+i| = \sqrt 2$) \to$\to$ |u| = \sqrt{\sqrt 2} = 2^{1/4}$|u| = \sqrt{\sqrt 2} = 2^{1/4}$ \to$\to$ u = 2^{1/4} * e^{i * 22.5}$u = 2^{1/4} * e^{i * 22.5}$
• Substitution:
  • z.B. z^4 + 2z^2 + 3 = 0$z^4 + 2z^2 + 3 = 0$
    • sei z^2 = u$z^2 = u$
    • dann gilt: u^2 + 2u + 3 = 0 \to ... \to u_{1,2} = 1 \pm i * \sqrt 2$u^2 + 2u + 3 = 0 \to ... \to u_{1,2} = 1 \pm i * \sqrt 2$
    • Rücksubstitution: z^2 = 1 + i * \sqrt 2 \to z = \sqrt{1 + i * \sqrt 2}$z^2 = 1 + i * \sqrt 2 \to z = \sqrt{1 + i * \sqrt 2}$ (Polardarstellung hier einsetzen...)

Potenzieren von z (Formel von de Moivre)

• (\cos(\varphi) + i * \sin(\varphi))^{n} = \cos(n * \varphi) + i * \sin(n * \varphi)$(\cos(\varphi) + i * \sin(\varphi))^{n} = \cos(n * \varphi) + i * \sin(n * \varphi)$
  • z.B. (\cos (\frac{\pi}{3}) - i * \sin(\frac{\pi}{3}))^{400} = \cos (400 * \frac{\pi}{3}) - i * \sin(400 * \frac{\pi}{3})$(\cos (\frac{\pi}{3}) - i * \sin(\frac{\pi}{3}))^{400} = \cos (400 * \frac{\pi}{3}) - i * \sin(400 * \frac{\pi}{3})$

Einheitswurzeln

• gesucht: alle Lösungen von x^n = 1 \in \mathbb{C}$x^n = 1 \in \mathbb{C}$
  • n$n$-te Einheitswurzeln: \Omega_n := \{e^{ik\frac{2\pi}{n}} \;|\; k = 0,1,...,n-1\} = \{\cos(k\frac{2\pi}{n}) + i * \sin(k\frac{2\pi}{n}) \;|\; k = 0,1,...,n-1\}$\Omega_n := \{e^{ik\frac{2\pi}{n}} \;|\; k = 0,1,...,n-1\} = \{\cos(k\frac{2\pi}{n}) + i * \sin(k\frac{2\pi}{n}) \;|\; k = 0,1,...,n-1\}$
• gesucht: alle Lösungen von x^n = z \in \mathbb{C}$x^n = z \in \mathbb{C}$
  • finde eine konkrete Lüsung x \in \mathbb{C}$x \in \mathbb{C}$ mit x^n = z$x^n = z$ über Polarkoordinaten
    • x = \sqrt[n]{r} * e^{i*\frac{\varphi}{n}} = \sqrt[n]{r} * (\cos(\frac{\varphi}{n}) + i * \sin(\frac{\varphi}{n}))$x = \sqrt[n]{r} * e^{i*\frac{\varphi}{n}} = \sqrt[n]{r} * (\cos(\frac{\varphi}{n}) + i * \sin(\frac{\varphi}{n}))$
  • multipliziere dieses x$x$ mit allen n$n$-ten Einheitswurzeln
    • z_k = \sqrt[n]{r} * e^{i*\frac{\varphi + k * 2\pi}{n}}$z_k = \sqrt[n]{r} * e^{i*\frac{\varphi + k * 2\pi}{n}}$ mit k = 0, 1, ... , n-1$k = 0, 1, ... , n-1$
    • alt. z_k = \sqrt[n]{r} * (\cos(\frac{\varphi + k * 2\pi}{n}) + i * \sin(\frac{\varphi + k * 2\pi}{n}))$z_k = \sqrt[n]{r} * (\cos(\frac{\varphi + k * 2\pi}{n}) + i * \sin(\frac{\varphi + k * 2\pi}{n}))$

Berechnung von komplexen Wurzeln

1. komplexe Zahl unter der Wurzel in Polardarstellung umformeln
   1.1 für Zahlen \in \R_{\geq0}$\in \R_{\geq0}$ ist \varphi = 0$\varphi = 0$
   1.2 für Zahlen \in \R_{< 0}$\in \R_{< 0}$ ist \varphi = \pi$\varphi = \pi$
2. wende Formel z^n = r*e^{i(\varphi + 2\pi k)}$z^n = r*e^{i(\varphi + 2\pi k)}$
   2.1. z = (r*e^{i(\varphi + 2\pi k)})^{\frac{1}{n}} = r^{\frac{1}{n}}*e^{i*{\frac{1}{n}}(\varphi + 2\pi k)} = \sqrt[n]r*e^{i*(\frac{\varphi + 2\pi k}{n})}$z = (r*e^{i(\varphi + 2\pi k)})^{\frac{1}{n}} = r^{\frac{1}{n}}*e^{i*{\frac{1}{n}}(\varphi + 2\pi k)} = \sqrt[n]r*e^{i*(\frac{\varphi + 2\pi k}{n})}$
   2.2 Radius wird potenziert, Winkel wird multipliziert

• z.B. z^4 = 1 + \sqrt3i$z^4 = 1 + \sqrt3i$
  • r = 2$r = 2$, \varphi = \arccos(1/2) = \frac{\pi}{3}$\varphi = \arccos(1/2) = \frac{\pi}{3}$
  • z^4 = 2 * e^{\frac{\pi}{3}i}$z^4 = 2 * e^{\frac{\pi}{3}i}$
  • beide Seiten mit \sqrt[4]\cdots$\sqrt[4]\cdots$ rechnen \to$\to$ Radius hoch 1/4$1/4$, Winkel mal 1/4$1/4$
    • z_0 = \sqrt[4]2 * e^{\frac{1}{4}\frac{\pi}{3}i} = \sqrt[4]2 * e^{\frac{\pi}{12}i}$z_0 = \sqrt[4]2 * e^{\frac{1}{4}\frac{\pi}{3}i} = \sqrt[4]2 * e^{\frac{\pi}{12}i}$
    • analog z_1, z_2, z_3$z_1, z_2, z_3$

Wichtige sin- und cos-Werte

Winkel (deg)	Winkel (rad)	\sin$\sin$	\cos$\cos$
0°$0°$	0$0$	0$0$	1$1$
30°$30°$	\frac{\pi}{6}$\frac{\pi}{6}$	\frac{1}{2}$\frac{1}{2}$	\frac{\sqrt 3}{2}$\frac{\sqrt 3}{2}$
45°$45°$	\frac{\pi}{4}$\frac{\pi}{4}$	\frac{1}{\sqrt 2}$\frac{1}{\sqrt 2}$	\frac{1}{\sqrt 2}$\frac{1}{\sqrt 2}$
60°$60°$	\frac{\pi}{3}$\frac{\pi}{3}$	\frac{\sqrt 3}{2}$\frac{\sqrt 3}{2}$	\frac{1}{2}$\frac{1}{2}$
90°$90°$	\frac{\pi}{2}$\frac{\pi}{2}$	1$1$	0$0$

BONUS: Umschreiben in Exponentialdarstellung

• Sei z = 10 * (\cos (\frac{\pi}{3}) - i * \sin(\frac{\pi}{3}))$z = 10 * (\cos (\frac{\pi}{3}) - i * \sin(\frac{\pi}{3}))$
• es gilt:
  • -\sin(\varphi) = \sin(-\varphi)$-\sin(\varphi) = \sin(-\varphi)$
  • \cos(-\varphi) = \cos(\varphi)$\cos(-\varphi) = \cos(\varphi)$
• daraus folgt:
  • z = 10 * (\cos (-\frac{\pi}{3}) + i * \sin(-\frac{\pi}{3})) \to$z = 10 * (\cos (-\frac{\pi}{3}) + i * \sin(-\frac{\pi}{3})) \to$ Polardarstellung

Lineare Gleichungssysteme und Matrizen

• m$m$ Gleichungen, n$n$ Variablen
  • Koeffizientenmatrix A$A$
    \begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}$\begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}$
  • erweiterte Koeffizientenmatrix (A \;|\; b)$(A \;|\; b)$
    \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} & | & b _ 1\\ \vdots & \ddots & \vdots & | & \vdots\\ a_{m,1} & \cdots & a_{m,n} & | & b_m \end{pmatrix}$\begin{pmatrix} a_{1,1} & \cdots & a_{1,n} & | & b _ 1\\ \vdots & \ddots & \vdots & | & \vdots\\ a_{m,1} & \cdots & a_{m,n} & | & b_m \end{pmatrix}$

Gaussches Eliminationsverfahren

• LGS auf Zeilenstufenform bringen, ohne die Lösungsmenge zu verändern
• elementare Zeilenumformungen:
  • Vertauschen zweier Zeilen
  • Multiplikation einer Zeile mit Faktor \lambda \neq 0$\lambda \neq 0$
  • Addition des \lambda$\lambda$-fachen einer Zeile zu einer anderen
• mögliche Formen der letzten Zeile(n) nach Anwendung des Gauß-Algorithmus:
  • (0 \cdots 0 \; | \; x)$(0 \cdots 0 \; | \; x)$ mit x \neq 0$x \neq 0$: nicht lösbar
  • (0 \cdots 0 \; | \; 0)$(0 \cdots 0 \; | \; 0)$: lösbar

Rang einer Matrix

• rg(m)$rg(m)$: Anzahl der nicht-null-Zeilen nach dem Anwenden des Gauß-Algorithmus
  • alt. Anzahl linear unabhängiger Spalten / Zeilen von A
• ein LGS ist genau dann lösbar, wenn rg(A) = rg(A \;|\; b)$rg(A) = rg(A \;|\; b)$; dann gilt:
  • Anzahl der frei wählbaren Variablen = n-rg(A)$n-rg(A)$ (n$n$ - Anzahl der Variablen)
  • LGS ist eindeutig lösbar, wenn n = rg(A)$n = rg(A)$ bzw. n = rg(A \;|\; b)$n = rg(A \;|\; b)$
    \begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ 0 & \cdots & a_{m,n} \end{pmatrix}$\begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ 0 & \cdots & a_{m,n} \end{pmatrix}$
  • LGS hat \infty$\infty$ Lösungen, wenn n > rg(A)$n > rg(A)$ bzw. n > rg(A \;|\; b)$n > rg(A \;|\; b)$
    \begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ 0 & \cdots & 0 \end{pmatrix}$\begin{pmatrix} a_{1,1} & \cdots & a_{1,n}\\ \vdots & \ddots & \vdots\\ 0 & \cdots & 0 \end{pmatrix}$
• Zeilenrang: Anzahl linear unabhängiger Zeilen von A
• Spaltenrang: Anzahl linear unabhängiger Spalten von A
• Zeilenrang = Spaltenrang = Rang

Homogene und inhomogene LGS

• homogene LGS

  • Ax=0$Ax=0$, oder b=0$b=0$
    • hat immer mindestens eine Lösung, die triviale Lösung 0
  • (A \;|\; 0)$(A \;|\; 0)$: das zu (A\;|\;b)$(A\;|\;b)$ gehörige homogene LGS
    \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} & | & 0\\ \vdots & \ddots & \vdots & | & \vdots\\ a_{m,1} & \cdots & a_{m,n} & | & 0 \end{pmatrix}$\begin{pmatrix} a_{1,1} & \cdots & a_{1,n} & | & 0\\ \vdots & \ddots & \vdots & | & \vdots\\ a_{m,1} & \cdots & a_{m,n} & | & 0 \end{pmatrix}$

• inhomogene LGS

  • Ax = b$Ax = b$, oder b \neq 0$b \neq 0$

• ein LGS hat immer entweder...

  • ...keine Lösung (inhomogenes LGS)
  • ...genau eine Lösung (inhomogenes LGS, homogenes LGS)
  • ...unendlich viele Lösungen (inhomogenes LGS, homogenes LGS)

• ist x_0$x_0$ eine Lösung eines inhomogenen LGS (x \in L_{A,b}$x \in L_{A,b}$), dann gilt L_{A,b} = x_0 + L_{A, 0}$L_{A,b} = x_0 + L_{A, 0}$

Rechnen mit Matrizen

• Matrix: rechteckiges Zahlenschema A \in K^{m \times n}$A \in K^{m \times n}$ (K - Körper)

  • m$m$ Zeilen, n$n$ Spalten
  • a_{i,j} \in A$a_{i,j} \in A$: Eintrag an Zeile i$i$, Spalte j$j$
    • z.B. a_{2,3} = 6$a_{2,3} = 6$ in K^{2 \times 3}$K^{2 \times 3}$ (Index fängt bei 1 an)
      \begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{pmatrix}$\begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{pmatrix}$

• Gleichheit von Matrizen: gleiche Anzahl von Zeilen und Spalten und an jeder Stelle müssen dieselben Koeffizienten liegen

Rechenoperationen

• Transponieren

  • sei A = \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}$A = \begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}$, dann gilt A^T = \begin{pmatrix} a_{1,1} & \cdots & a_{m,1} \\ \vdots & \ddots & \vdots \\ a_{1,n} & \cdots & a_{m,n} \end{pmatrix}$A^T = \begin{pmatrix} a_{1,1} & \cdots & a_{m,1} \\ \vdots & \ddots & \vdots \\ a_{1,n} & \cdots & a_{m,n} \end{pmatrix}$
    • z.B. \begin{pmatrix} 1 & 2 & 3 \end{pmatrix}^T = \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}$\begin{pmatrix} 1 & 2 & 3 \end{pmatrix}^T = \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}$
  • Regeln:
    • (A+B)^T = A^T + B^T$(A+B)^T = A^T + B^T$
    • (A^T)^T = A$(A^T)^T = A$
    • (\lambda A)^T = \lambda A^T$(\lambda A)^T = \lambda A^T$
    • für A, B: A \in K^{m \times n}, B \in K^{n \times p}$A, B: A \in K^{m \times n}, B \in K^{n \times p}$ gilt (AB)^T = B^T A^T$(AB)^T = B^T A^T$
  • symmetrische Matrix (nur quadratisch): A^T = A$A^T = A$
    • z.B. \begin{pmatrix} 1 & 2 & 3\\ 2 & 4 & 5\\ 3 & 5 & 6 \end{pmatrix}^T = \begin{pmatrix} 1 & 2 & 3\\ 2 & 4 & 5\\ 3 & 5 & 6 \end{pmatrix}$\begin{pmatrix} 1 & 2 & 3\\ 2 & 4 & 5\\ 3 & 5 & 6 \end{pmatrix}^T = \begin{pmatrix} 1 & 2 & 3\\ 2 & 4 & 5\\ 3 & 5 & 6 \end{pmatrix}$

• Addition

  • für A = (a_{i,j}), B = (b_{i,j}) \in K^{m\times n}$A = (a_{i,j}), B = (b_{i,j}) \in K^{m\times n}$ gilt A + B = (a_{i,j} + b_{i,j})$A + B = (a_{i,j} + b_{i,j})$
    • Koeffizienten an selber Stelle addieren, Dimensionen der beiden Matrizen müssen gleich sein
  • Regeln (abelsche Gruppe):
    • Abgeschlossenheit: A + B \in K^{m\times n}$A + B \in K^{m\times n}$
    • Assoziativität: (A + B) + C = A + (B + C)$(A + B) + C = A + (B + C)$
    • neutrales Element: \exists 0: A + 0 = A = 0 + A$\exists 0: A + 0 = A = 0 + A$
    • Inverses: \forall A \exists B: A + B = 0 = B + A$\forall A \exists B: A + B = 0 = B + A$ (B = -A$B = -A$)
    • Kommutativität: A + B = B + A$A + B = B + A$

• skalare Multiplikation

  • für \mu, \lambda \in K; A, B \in K^{m\times n}$\mu, \lambda \in K; A, B \in K^{m\times n}$ gilt \lambda A = (\lambda a_{i,j})$\lambda A = (\lambda a_{i,j})$
    • jeder Koeffizient wird mit Lambda multipliziert
  • Regeln:
    • Assoziativität: (\mu \lambda) A = \mu (\lambda A)$(\mu \lambda) A = \mu (\lambda A)$
    • Distributivität: (\mu + \lambda)A = \mu A + \lambda A$(\mu + \lambda)A = \mu A + \lambda A$
    • II. Distributivitätsgesetz: \lambda(A + B) = \lambda A + \lambda B$\lambda(A + B) = \lambda A + \lambda B$
    • neutrales Element: 1 * A = A$1 * A = A$

• Multiplikation

  • (z_1 ... z_n) * \begin{pmatrix} s_1\\ \vdots\\ s_n \end{pmatrix} = \sum_{i=1}^{n}z_is_i$(z_1 ... z_n) * \begin{pmatrix} s_1\\ \vdots\\ s_n \end{pmatrix} = \sum_{i=1}^{n}z_is_i$ (Zeile muss so lang wie Spalte sein!)
  • gilt nur für A, B: A \in K^{m \times n}, B \in K^{n \times p}$A, B: A \in K^{m \times n}, B \in K^{n \times p}$
  • Regeln:
    • Multiplikation ist nicht kommutativ und bildet nicht eine Gruppe (da es nicht unbedingt ein Inverses gibt)
    • Abgeschlossenheit: AB \in K^{n \times n}$AB \in K^{n \times n}$
    • Assoziativität: (AB)C = A(BC)$(AB)C = A(BC)$
    • neutrales Element: \exists E_n: E_nA = A = AE_n$\exists E_n: E_nA = A = AE_n$
    • Distributivität: (A+B)C = AC + BC$(A+B)C = AC + BC$ und A(B+C) = AB + AC$A(B+C) = AB + AC$

• Invertieren

  • Voraussetzung: A \in K^{n \times n}$A \in K^{n \times n}$ quadratisch
    • eine Matrix mit einer Nullzeile ist nie invertierbar
  • Inverses bestimmen:
    • stelle (A | E_n)$(A | E_n)$ auf
    • wende Gauß-Algorithmus an, um E_n$E_n$ auf der linken Seite herauszubekommen
    • Ergebnis: (E_n | A^{-1})$(E_n | A^{-1})$
  • Regeln:
    • AA^{-1} = E_n$AA^{-1} = E_n$
    • ABB^{-1}A^{-1}=E_n$ABB^{-1}A^{-1}=E_n$
    • (A^{-1})^T = (A^T)^{-1}$(A^{-1})^T = (A^T)^{-1}$
    • (\lambda A)^{-1} = \frac{1}{\lambda}A^{-1}$(\lambda A)^{-1} = \frac{1}{\lambda}A^{-1}$

Elementarmatrizen

• Permutationsmatrix
  \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 3 & 3 & 3\\ 2 & 2 & 2 \end{pmatrix}$\begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 3 & 3 & 3\\ 2 & 2 & 2 \end{pmatrix}$
• Multiplikation einer Zeile mit \lambda \neq 0$\lambda \neq 0$
  \begin{pmatrix} 1 & 0 & 0\\ 0 & \varphi & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 2\varphi & 2\varphi & 2\varphi\\ 3 & 3 & 3 \end{pmatrix}$\begin{pmatrix} 1 & 0 & 0\\ 0 & \varphi & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 2\varphi & 2\varphi & 2\varphi\\ 3 & 3 & 3 \end{pmatrix}$
• Addition des \lambda$\lambda$-fachen einer Zeile zu einer anderen Zeile
  \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 3\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 11 & 11 & 11\\ 3 & 3 & 3 \end{pmatrix}$\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 3\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1\\ 2 & 2 & 2\\ 3 & 3 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1\\ 11 & 11 & 11\\ 3 & 3 & 3 \end{pmatrix}$ (+ 3 * III)

Kern einer Matrix

• Lösungsmenge des homogenen linearen Gleichungssystems Ax = 0$Ax = 0$
  • anders: womit muss man eine Matrix A$A$ multiplizieren, damit man den Nullvektor bekommt?
  • formell: \ker(A) = \{v \in \mathbb{K}^n \; | \; Av = 0\} \subseteq \mathbb{K}^n$\ker(A) = \{v \in \mathbb{K}^n \; | \; Av = 0\} \subseteq \mathbb{K}^n$
• Eigenschaften:
  • der Kern einer Matrix A \in \mathbb{K}^{m \times n}$A \in \mathbb{K}^{m \times n}$ ist ein Untervektorraum von \mathbb{K}^n$\mathbb{K}^n$
  • \dim(\ker(A)) = n - rg(A)$\dim(\ker(A)) = n - rg(A)$
  • für quadratische Matrizen: \dim(\ker(A))$\dim(\ker(A))$ = Anzahl der Nullzeilen in Zeilenstufenform
• REZEPT: Bestimmen des Kerns: (p. 157)
  • löse das homogene LGS (A \; | \; 0)$(A \; | \; 0)$
  • gebe Lösung als Basis an, da die Lösungsmenge ein Vektorraum ist
• Beispiel:
  f(x)=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} =\begin{pmatrix} x_1 \\ x_2 \\ 0 \end{pmatrix} $f(x)=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} =\begin{pmatrix} x_1 \\ x_2 \\ 0 \end{pmatrix}$
  • die Abbildung f$f$ bildet genau die Vektoren der Form x = \begin{pmatrix} 0 \\ 0 \\ \lambda\end{pmatrix}, \lambda \in \R$x = \begin{pmatrix} 0 \\ 0 \\ \lambda\end{pmatrix}, \lambda \in \R$ auf den Nullvektor ab
  • folglich ist \ker f =\left\{\begin{pmatrix} 0 \\ 0 \\ \lambda\end{pmatrix}, \lambda \in \R\right\}$\ker f =\left\{\begin{pmatrix} 0 \\ 0 \\ \lambda\end{pmatrix}, \lambda \in \R\right\}$

Determinante einer quadratischen Matrix

• \det(A) = \sum_{i=1}^n(-1)^{i+1}a_{i1} \det(A_{i1})$\det(A) = \sum_{i=1}^n(-1)^{i+1}a_{i1} \det(A_{i1})$
  • \det(A) = a_{11}\det(A_{11}) - a_{21}\det(A_{21}) + ... + (-1)^{n+1}a_{n1}\det(A_{n1})$\det(A) = a_{11}\det(A_{11}) - a_{21}\det(A_{21}) + ... + (-1)^{n+1}a_{n1}\det(A_{n1})$
• im Fall n = 2$n = 2$: \det(A) = a_{11}a_{22} - a_{12}a_{21}$\det(A) = a_{11}a_{22} - a_{12}a_{21}$
• im Fall n = 3$n = 3$: \det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - (a_{13}a_{22}a_{31} + a_{23}a_{32}a_{11} + a_{33}a_{12}a_{21})$\det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - (a_{13}a_{22}a_{31} + a_{23}a_{32}a_{11} + a_{33}a_{12}a_{21})$ (Regel von Sarrus)
• allgemeine Berechnung für quadratische Matrizen A = (a_{ij})$A = (a_{ij})$:
  • Entwicklung nach j$j$-ter Spalte: \det(A) = \sum_{i=1}^n (-1)^{i+j}a_{ij}\det(A_{ij})$\det(A) = \sum_{i=1}^n (-1)^{i+j}a_{ij}\det(A_{ij})$
  • Entwicklung nach i$i$-ter Zeile: \det(A) = \sum_{j=1}^n (-1)^{i+j}a_{ij}\det(A_{ij})$\det(A) = \sum_{j=1}^n (-1)^{i+j}a_{ij}\det(A_{ij})$
• REZEPT: Determinante bestimmen für Matrizen mit n \geq 3$n \geq 3$:
  1. hat A$A$ zwei gleiche Zeilen oder Spalten bzw. zwei Zeilen oder Spalten, die Vielfache voneinander sind, gilt \det(A) = 0$\det(A) = 0$
  2. hat A$A$ Blockdreiecksgestalt A = \begin{pmatrix} B & 0 \\ C & D \end{pmatrix}$A = \begin{pmatrix} B & 0 \\ C & D \end{pmatrix}$ oder A = \begin{pmatrix} B & C \\ 0 & D \end{pmatrix}$A = \begin{pmatrix} B & C \\ 0 & D \end{pmatrix}$, dann \det(A) = \det(B) \det(D)$\det(A) = \det(B) \det(D)$
  3. wenn es eine Zeile bzw. Spalte mit vielen Nullen gibt, dann entwickle nach dieser Zeile bzw. Spalte
  4. wenn nicht, dann erzeuge Nullen durch Umformungen und entwickle nach dieser Zeile oder Spalte
  5. beginne von vorne
• Eigenschaften:
  • \det(A) = \det(A^T)$\det(A) = \det(A^T)$
  • \det(A \cdot B) = \det(A) \det(B)$\det(A \cdot B) = \det(A) \det(B)$
  • \det(A^{-1}) = \frac{1}{\det(A)}$\det(A^{-1}) = \frac{1}{\det(A)}$
  • \det(A^k)=(\det(A))^k$\det(A^k)=(\det(A))^k$
  • \det(\lambda A) = \lambda^n \det (A)$\det(\lambda A) = \lambda^n \det (A)$
  • ist A$A$ obere oder untere Dreiecksmatrix, so gilt \det(A) = \lambda_1 \cdot ... \cdot \lambda_n$\det(A) = \lambda_1 \cdot ... \cdot \lambda_n$
    • A = \begin{pmatrix} \lambda_1 & & * \\ & \ddots & \\ 0 & & \lambda_n \end{pmatrix}$A = \begin{pmatrix} \lambda_1 & & * \\ & \ddots & \\ 0 & & \lambda_n \end{pmatrix}$ bzw. A = \begin{pmatrix} \lambda_1 & & 0 \\ & \ddots & \\ * & & \lambda_n \end{pmatrix}$A = \begin{pmatrix} \lambda_1 & & 0 \\ & \ddots & \\ * & & \lambda_n \end{pmatrix}$
  • hat A$A$ Blockdreiecksgestalt mit quadratischen Matrizen B$B$ und D$D$ und passenden 0 und C$C$, so gilt \det(A) = \det(B) \det(D)$\det(A) = \det(B) \det(D)$
    • A = \begin{pmatrix} B & 0 \\ C & D\end{pmatrix}$A = \begin{pmatrix} B & 0 \\ C & D\end{pmatrix}$ bzw. A = \begin{pmatrix} B & C \\ 0 & D\end{pmatrix}$A = \begin{pmatrix} B & C \\ 0 & D\end{pmatrix}$
  • eine Matrix ist genau dann invertierbar, wenn \det(A) \neq 0$\det(A) \neq 0$
  • ist A$A$ invertierbar, so gilt \det(A^{-1}) = (\det(A))^{-1}$\det(A^{-1}) = (\det(A))^{-1}$
  • wenn A$A$ zwei gleiche Spalten oder gleiche Zeilen hat (oder Linearkombinationen davon), gilt \det(A) = 0$\det(A) = 0$
  • unter elementaren Zeilen- bzw. Spaltenumformungen:
    • Vertauschen zweier Zeilen oder Spalten verändert das Vorzeichen der Determinante
      • \det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = -\det\begin{pmatrix}\vdots \\ z_l \\ \vdots \\ z_k \\ \vdots \end{pmatrix}$\det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = -\det\begin{pmatrix}\vdots \\ z_l \\ \vdots \\ z_k \\ \vdots \end{pmatrix}$
    • Multiplikation einer Zeile oder Spalte mit \lambda$\lambda$ bewirkt eine Multiplikation der Determinante mit \lambda$\lambda$
      • \det\begin{pmatrix}\vdots \\ \lambda z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = \lambda\det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix}$\det\begin{pmatrix}\vdots \\ \lambda z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = \lambda\det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix}$
    • Addition des \lambda$\lambda$-Fachen einer Zeile oder Spalte zu einer anderen Zeile oder Spalte ändert die Determinante nicht
      • \det\begin{pmatrix}\vdots \\ z_k + \lambda z_l \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = \det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix}$\det\begin{pmatrix}\vdots \\ z_k + \lambda z_l \\ \vdots \\ z_l \\ \vdots \end{pmatrix} = \det\begin{pmatrix}\vdots \\ z_k \\ \vdots \\ z_l \\ \vdots \end{pmatrix}$

Orthogonale Matrizen

• eine symmetrische Matrix A$A$ ist orthogonal, wenn A^TA = E_n$A^TA = E_n$
• Eigenschaften:
  • A$A$ ist invertierbar
  • A^{-1} = A^T$A^{-1} = A^T$
  • die Spalten bzw. Zeilen von A$A$ bilden eine ONB des \R^n$\R^n$
  • \det(A) = \pm 1$\det(A) = \pm 1$
  • A$A$ ist längenerhaltend, d.h. ||Av|| = ||v||$||Av|| = ||v||$ für jedes v \in \R^n$v \in \R^n$
  • das Produkt orthogonaler Matrizen ist orthogonal

Darstellungsmatrizen

• seien V$V$ und W$W$ endlichdimensionale K$K$-Vektorräume mit...
  • \dim(V) = n$\dim(V) = n$ und B = (b_1, ..., b_n)$B = (b_1, ..., b_n)$ eine Basis von V$V$
  • \dim(W) = m$\dim(W) = m$ und C = (c_1, ..., c_m)$C = (c_1, ..., c_m)$ eine Basis von W$W$
• ist f : V \to W$f : V \to W$ linear, so nennt man die m \times n$m \times n$-Matrix _CM(f)_B = (_Cf(b_1), ..., _Cf(b_n))$_CM(f)_B = (_Cf(b_1), ..., _Cf(b_n))$ die Darstellungsmatrix von f$f$ bzgl. B und C
  • Satz: in der i$i$-ten Spalte der Darstellungsmatrix steht der Koordinatenvektor des Bildes des i$i$-ten Basisvektors
• zu jeder linearen Abbildung f : K^n \to K^m$f : K^n \to K^m$ gibt es eine Matrix A \in K^{m \times n}$A \in K^{m \times n}$ mit f_A(v) = Av$f_A(v) = Av$
  • die Matrix A$A$ erhält man durch A = \; _{E_m}M(f)_{E_n} = (f(e_1), ..., f(e_n))$A = \; _{E_m}M(f)_{E_n} = (f(e_1), ..., f(e_n))$
• Eigenschaften:
  • f$f$ ist injektiv \iff$\iff$ \ker(A) = \{0\}$\ker(A) = \{0\}$
  • f$f$ ist surjektiv \iff$\iff$ \text{rg}(A) = m$\text{rg}(A) = m$
  • f$f$ ist bijektiv \iff$\iff$ A$A$ invertierbar
• Beispiel für \R^3$\R^3$:
  • f : \R^2 \to \R^3$f : \R^2 \to \R^3$, f(x,y) = \begin{pmatrix} x + y \\ x - y \\ 2x \end{pmatrix}$f(x,y) = \begin{pmatrix} x + y \\ x - y \\ 2x \end{pmatrix}$
  • E_2 = \left( b_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, b_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right)$E_2 = \left( b_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, b_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right)$, E_3 = \left( c_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, c_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, c_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right)$E_3 = \left( c_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, c_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, c_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right)$
  • dann gilt: f(b_1) = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} = c_1 + c_2 + 2c_3 \to \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$f(b_1) = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} = c_1 + c_2 + 2c_3 \to \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$ und f(b_2) = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} = c_1 - c_2 \to \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}$f(b_2) = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} = c_1 - c_2 \to \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}$
  • _{E_3}M(f)_{E_2} = \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ 2 & 0 \end{pmatrix}$_{E_3}M(f)_{E_2} = \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ 2 & 0 \end{pmatrix}$

Darstellungsmatrix der Verkettungen

• für lineare Abbildungen f : V \to W$f : V \to W$ und g : W \to U$g : W \to U$ mit den Basen B = (b_1, ..., b_n) \subseteq V$B = (b_1, ..., b_n) \subseteq V$, C = (c_1, ..., c_m) \subseteq W$C = (c_1, ..., c_m) \subseteq W$ und D = (d_1, ..., d_r) \subseteq U$D = (d_1, ..., d_r) \subseteq U$ und den Darstellungsmatrizen _CM(f)_B$_CM(f)_B$ und _DM(g)_C$_DM(g)_C$ gilt:
  • _DM(g \circ f)_B = _DM(g)_C \; _CM(f)_B$_DM(g \circ f)_B = _DM(g)_C \; _CM(f)_B$

Basistransformation

• gegeben:
  • lineare Abbildung f : V \to W$f : V \to W$
  • zwei Basen von V$V$
    • B = (b_1, ..., b_n)$B = (b_1, ..., b_n)$
    • B' = (b_1', ..., b_n')$B' = (b_1', ..., b_n')$
  • zwei Basen von W$W$
    • C = (c_1, ..., c_m)$C = (c_1, ..., c_m)$
    • C' = (c_1', ..., c_m')$C' = (c_1', ..., c_m')$
• dann gilt die Basistransformationsformel:
  • _{C'}M(f)_{B'} \; = \; _{C'}M(\text{Id})_C \; _CM(f)_B \; _BM(\text{Id})_{B'}$_{C'}M(f)_{B'} \; = \; _{C'}M(\text{Id})_C \; _CM(f)_B \; _BM(\text{Id})_{B'}$
  • _{C'}M(\text{Id})_C = (_{C'}c_1, ... _{C'}c_m) \in K^{m \times m}$_{C'}M(\text{Id})_C = (_{C'}c_1, ... _{C'}c_m) \in K^{m \times m}$
  • _{B'}M(\text{Id})_B = (_{B'}b_1, ... _{B'}b_n) \in K^{n \times n}$_{B'}M(\text{Id})_B = (_{B'}b_1, ... _{B'}b_n) \in K^{n \times n}$
• (!) Sonderfall: für f : K^n \to K^n$f : K^n \to K^n$ mit f(v) = Av$f(v) = Av$ gilt...
  • _BM(f)_B = B^{-1}AB$_BM(f)_B = B^{-1}AB$
  • multipliziere A$A$ mit jedem Basisvektor b_i$b_i$ und trage Koordinatenvektor in Ergebnismatrix ein
• REZEPT: Bestimmen einer Darstellungsmatrix _BM(f)_B$_BM(f)_B$
  • gegeben: lineare Abbildung f : V \to V$f : V \to V$ mit geordneter Basis B = (b_1, ..., b_n)$B = (b_1, ..., b_n)$
  • Fall V = K^n$V = K^n$ und B = E_n$B = E_n$: A = (f(e_1), ..., f(e_n))$A = (f(e_1), ..., f(e_n))$
  • bestimme für jedes i = 1, ..., n$i = 1, ..., n$ den Koordinatenvektor _Bf(b_i) = (\lambda_1, ..., \lambda_n)^T$_Bf(b_i) = (\lambda_1, ..., \lambda_n)^T$ aus f(b_i) = \lambda_1b_1 + ... + \lambda_nb_n$f(b_i) = \lambda_1b_1 + ... + \lambda_nb_n$ und erhalte A = (_Bf(b_1), ..., _Bf(b_n))$A = (_Bf(b_1), ..., _Bf(b_n))$
  • falls eine Darstellungsmatrix _CM(f)_C$_CM(f)_C$ bekannt ist, so gilt A = S^{-1} \; _CM(f)_C \; S$A = S^{-1} \; _CM(f)_C \; S$ mit S \; = \; _CM(\text{Id})_B$S \; = \; _CM(\text{Id})_B$

Eigenwerte, Eigenvektoren, Diagonalisieren

• gegeben: quadratische Matrix A \in K^{n \times n}$A \in K^{n \times n}$ mit Av = \lambda v, v \neq 0, \lambda \in K$Av = \lambda v, v \neq 0, \lambda \in K$
  • v \in K \backslash \{0\}$v \in K \backslash \{0\}$: Eigenvektor von A$A$ zum Eigenwert \lambda$\lambda$
  • \lambda$\lambda$: Eigenwert von A$A$ mit Eigenvektor v \in K \backslash \{0\}$v \in K \backslash \{0\}$
• ist \lambda$\lambda$ ein Eigenwert von A$A$, so nennt man den Untervektorraum \text{Eig}_A(\lambda) = \{v \in K^n \; | \; Av = \lambda v\}$\text{Eig}_A(\lambda) = \{v \in K^n \; | \; Av = \lambda v\}$ den Eigenraum von A$A$ zum Eigenwert \lambda$\lambda$ und \dim(\text{Eig}_A(\lambda))$\dim(\text{Eig}_A(\lambda))$ die geometrische Vielfachheit des Eigenwerts \lambda$\lambda$
  • \text{geo}(\lambda) = \dim(\text{Eig}_A(\lambda))$\text{geo}(\lambda) = \dim(\text{Eig}_A(\lambda))$
  • in einer symmetrischen Matrix stehen die Eigenräume senkrecht aufeinander
• Diagonalisieren einer Matrix:
  • eine quadratische Matrix A \in K^{n \times n}$A \in K^{n \times n}$ ist diagonalisierbar, wenn es eine invertierbare Matrix B \in K^{n \times n}$B \in K^{n \times n}$ gibt, so dass D = B^{-1}AB$D = B^{-1}AB$ eine Diagonalmatrix (Diagonalform zu A$A$) ist
  • D = diag(\lambda_1, ... , \lambda_n)$D = diag(\lambda_1, ... , \lambda_n)$
  • B = (b_1, ..., b_n)$B = (b_1, ..., b_n)$ (geordnete Basis)
• das charakteristische Polynom einer Matrix:
  • \chi_A = \det(A - \lambda E_n)$\chi_A = \det(A - \lambda E_n)$
  • zerfällt in Linearfaktoren: (\lambda_1 - \lambda)^{\nu_1} ... (\lambda_r - \lambda)^{\nu_r}$(\lambda_1 - \lambda)^{\nu_1} ... (\lambda_r - \lambda)^{\nu_r}$
  • \lambda_i$\lambda_i$ sind die verschiedenen Eigenwerte von A$A$
  • man nennt die Potenz \nu_i$\nu_i$ die algebraische Vielfachheit des Eigenwerts \lambda_i$\lambda_i$, geschrieben \text{alg}(\lambda_i) = \nu_i$\text{alg}(\lambda_i) = \nu_i$
  • wenn A$A$ eine symmetrische Matrix ist, dann ist rg(A)$rg(A)$ gleich der Anzahl der nicht-nullen Eigenwerten
• TIPP: Eigenwerte für A \in \R^{2 \times 2}$A \in \R^{2 \times 2}$:
  • \lambda_{1,2} = m \pm \sqrt{m^2 - p}$\lambda_{1,2} = m \pm \sqrt{m^2 - p}$
    • m$m$ (mean) = \frac{Spur(A)}{2}$\frac{Spur(A)}{2}$
    • p$p$ (product) = \det(A)$\det(A)$
• Kriterium zur Diagonalisierbarkeit:
  • eine quadratische Matrix A$A$ ist genau dann diagonalisierbar, wenn das charakteristische Polynom \chi_A$\chi_A$ in Linearfaktoren zerfällt und \text{alg}(\lambda) = \text{geo}(\lambda)$\text{alg}(\lambda) = \text{geo}(\lambda)$ für jeden Eigenwert \lambda$\lambda$ gilt
  • jede Matrix A \in K^{n \times n}$A \in K^{n \times n}$ mit n$n$ verschiedenen Eigenwerten ist diagonalisierbar
• REZEPT: Diagonalisieren einer Matrix A \in K^{n \times n}$A \in K^{n \times n}$
  • bestimme das charakteristische Polynom \chi_A$\chi_A$ und zerlege es in Linearfaktoren
    • es gilt \nu_1 + ... + \nu_r = n$\nu_1 + ... + \nu_r = n$
    • es sind \lambda_i$\lambda_i$ die verschiedenen Eigenwerte mit \text{alg}(\lambda_i) = \nu_i$\text{alg}(\lambda_i) = \nu_i$
    • ist \chi_A$\chi_A$ nicht vollständig in Linearfaktoren zerlegbar, dann ist A$A$ nicht diagonalisierbar
  • bestimme zu jedem Eigenwert \lambda_i$\lambda_i$ den Eigenraum \text{Eig}_A(\lambda_i)$\text{Eig}_A(\lambda_i)$ durch Angabe einer Basis B_i$B_i$
    • \text{Eig}_A(\lambda_i) = \ker(A - \lambda_iE_n) = \lang B_i \rang$\text{Eig}_A(\lambda_i) = \ker(A - \lambda_iE_n) = \lang B_i \rang$
    • es gilt |B_i| = \text{geo}(\lambda_i)$|B_i| = \text{geo}(\lambda_i)$
    • gilt \text{geo}(\lambda_i) \neq \text{alg}(\lambda_i)$\text{geo}(\lambda_i) \neq \text{alg}(\lambda_i)$ für ein i$i$, dann ist A$A$ nicht diagonalisierbar
  • es gilt B = \bigcup B_i$B = \bigcup B_i$, erhalte dann D = B^{-1}AB$D = B^{-1}AB$
    • alt. berechne Ab_i$Ab_i$ mit D$D$ als Koordinatenvektoren davon
• Eigenschaften:
  • \det(A) = \prod \lambda_i$\det(A) = \prod \lambda_i$ (Produkt der Eigenwerte)
  • \text{Spur}(A) = \sum \lambda_i$\text{Spur}(A) = \sum \lambda_i$ (Summe der Eigenwerte = Summe der Elemente auf der Diagonale)

Orthogonales Diagonalisieren

• ist A \in \R^{n \times n}$A \in \R^{n \times n}$ eine reelle, symmetrische Matrix mit A^T = A$A^T = A$, dann gilt:
  • A$A$ ist diagonalisierbar
  • alle Eigenwerte von A$A$ sind reell
  • Eigenvektoren zu verschiedenen Eigenwerten stehen senkrecht aufeinander (bzg. SSP \lang v, w \rang = v^Tw$\lang v, w \rang = v^Tw$)
  • die A$A$ diagonalisierende Matrix B$B$ kann orthogonal gewählt werden, d.h. D = B^{-1}AB = B^TAB$D = B^{-1}AB = B^TAB$
    • wähle ONB B$B$ so, dass die Vektoren innerhalb der Basen B_i$B_i$ auch orthogonal (und normiert) zueinander sind (Kreuzprodukt)

Gerschgorinkreise

• die n$n$ Eigenwerte einer Matrix A \in \mathbb{C}^{n \times n}$A \in \mathbb{C}^{n \times n}$ liegen in den n$n$ Gerschgorinkreisen:
  • K_i = \{z \in \mathbb{C} \; | \; |z - a_{ii}| \leq \sum_{j = 1, j \neq i}^n |a_{ij}|\}$K_i = \{z \in \mathbb{C} \; | \; |z - a_{ii}| \leq \sum_{j = 1, j \neq i}^n |a_{ij}|\}$
• wenn 0 kein EW sein kann (0 nicht in einem Gerschgorinkreis enthalten), dann ist A$A$ invertierbar
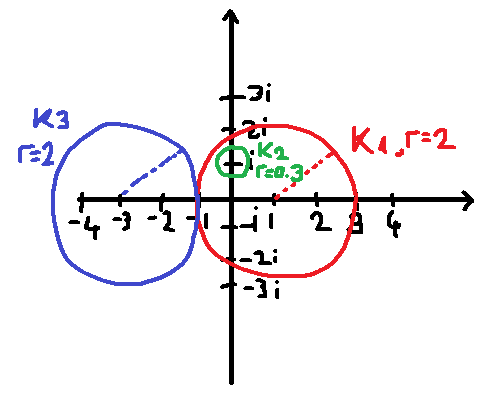
• Beispiel:
  • A = \begin{pmatrix} 1 & 0 & 2 \\ 0.1 & i & 0.2 \\ -1 & 1 & -3 \end{pmatrix}$A = \begin{pmatrix} 1 & 0 & 2 \\ 0.1 & i & 0.2 \\ -1 & 1 & -3 \end{pmatrix}$
  • K_1 = \{z \in \mathbb{C} \; | \; |z-1| \leq 0 + 2\}$K_1 = \{z \in \mathbb{C} \; | \; |z-1| \leq 0 + 2\}$
  • K_2 = \{z \in \mathbb{C} \; | \; |z-i| \leq 0.1 + 0.2\}$K_2 = \{z \in \mathbb{C} \; | \; |z-i| \leq 0.1 + 0.2\}$
  • K_3 = \{z \in \mathbb{C} \; | \; |z+3| \leq |-1| + 1\}$K_3 = \{z \in \mathbb{C} \; | \; |z+3| \leq |-1| + 1\}$
    

Singulärwertzerlegung

• A = U \Sigma V^T$A = U \Sigma V^T$
• REZEPT: Bestimmen der Singulärwertzerlegung:
  • bestimme Eigenwerte \lambda_1, ..., \lambda_n$\lambda_1, ..., \lambda_n$ von A^TA$A^TA$ und sortiere die ersten r$r$ absteigend (\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_r$\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_r$)
  • bestimme ONB V = (\nu_1, ..., \nu_n)$V = (\nu_1, ..., \nu_n)$ aus Eigenvektoren von A^TA$A^TA$
  • setze \sigma_i = \sqrt{\lambda_i}$\sigma_i = \sqrt{\lambda_i}$ und erhalte daraus \Sigma$\Sigma$
  • bestimme u_1, ..., u_r$u_1, ..., u_r$ aus u_i = \frac{1}{\sigma_i}A\nu_i$u_i = \frac{1}{\sigma_i}A\nu_i$ soweit möglich und ergänze sie falls r < m$r < m$ zu einer ONB bzw. orthogonalen Matrix U = (u_1, ..., u_m)$U = (u_1, ..., u_m)$

Definitheit symmterischer Matrizen

• allgemein:
  • positiv definit, wenn v^TAv > 0$v^TAv > 0$ für alle v \in \R^n \backslash \{0\}$v \in \R^n \backslash \{0\}$
  • negativ definit, wenn v^TAv < 0$v^TAv < 0$ für alle v \in \R^n \backslash \{0\}$v \in \R^n \backslash \{0\}$
  • positiv semidefinit, wenn v^TAv \geq 0$v^TAv \geq 0$ für alle v \in \R^n \backslash \{0\}$v \in \R^n \backslash \{0\}$
  • negativ semidefinit, wenn v^TAv \leq 0$v^TAv \leq 0$ für alle v \in \R^n \backslash \{0\}$v \in \R^n \backslash \{0\}$
  • indefinit, wenn es Vektoren mit v^TAv > 0$v^TAv > 0$ und w^TAw < 0$w^TAw < 0$ existieren
• Eigenwertkriterium:
  • positiv definit, wenn alle Eigenwerte positiv sind
  • negativ definit, wenn alle Eigenwerte negativ sind
  • positiv semidefinit, wenn alle Eigenwerte positiv oder null sind
  • negativ semidefinit, wenn alle Eigenwerte negativ oder null sind
  • indefinit, wenn A$A$ positive und negative Eigenwerte hat
• REZEPT: Trick für 2 \times 2$2 \times 2$-Matrizen der Form A = \begin{pmatrix} a & b \\ b & c \end{pmatrix}$A = \begin{pmatrix} a & b \\ b & c \end{pmatrix}$:
  • bestimme \det(A) = ac - b^2$\det(A) = ac - b^2$ und \text{Spur}(A) = a + c$\text{Spur}(A) = a + c$
    • wenn \det(A) < 0$\det(A) < 0$, so ist A$A$ indefinit
    • wenn \det(A) = 0$\det(A) = 0$ und \text{Spur}(A) \geq 0$\text{Spur}(A) \geq 0$, so ist A$A$ positiv semidefinit
    • wenn \det(A) = 0$\det(A) = 0$ und \text{Spur}(A) \leq 0$\text{Spur}(A) \leq 0$, so ist A$A$ negativ semidefinit
    • wenn \det(A) > 0$\det(A) > 0$ und \text{Spur}(A) > 0$\text{Spur}(A) > 0$, so ist A$A$ positiv definit
    • wenn \det(A) > 0$\det(A) > 0$ und \text{Spur}(A) < 0$\text{Spur}(A) < 0$, so ist A$A$ negativ definit

Gruppen und Ringe

Gruppen

• eine Menge G$G$ mit innerer Verknüpfung G \times G \to G$G \times G \to G$ heißt Gruppe, falls folgendes gilt:
  1. Abgeschlossenheit: G \times G \to G$G \times G \to G$
  2. Assoziativität: \forall \; a,b,c \in G: a \circ (b \circ c) = (a \circ b) \circ c$\forall \; a,b,c \in G: a \circ (b \circ c) = (a \circ b) \circ c$
  3. neutrales Element: \exists \; e \in G: e \circ a = a = a \circ e$\exists \; e \in G: e \circ a = a = a \circ e$ (eindeutig!)
  4. Inverses: \forall \; a \in G \; \exists \; b \in G: a \circ b = e = b \circ a$\forall \; a \in G \; \exists \; b \in G: a \circ b = e = b \circ a$ mit b = a^{-1}$b = a^{-1}$ (eindeutig!)
• eine Gruppe heißt abelsch, wenn diese kommutativ ist (\forall a,b \in G: a + b = b + a$\forall a,b \in G: a + b = b + a$)
• "Gruppen-Sudoku-Regel": in den Spalten und Zeilen einer Gruppentafel kann jedes Element jeweils nur genau einmal stehen
• REZEPT: eine Teilmenge U \subseteq G$U \subseteq G$ heißt Untergruppe von G (geschrieben U \leq G$U \leq G$), falls folgendes gilt:
  1. U$U$ Teilmenge von G$G$: U \subseteq G$U \subseteq G$
  2. neutrales Element von G$G$ in U$U$: e \in U$e \in U$ ("nicht leer")
  3. Abgeschlossenheit bzgl. U$U$: \forall u, v \in U : u \circ v \in U$\forall u, v \in U : u \circ v \in U$
  4. Abgeschlossenheit bzgl. inverses Element: \forall u \in U : u^{-1} \in U$\forall u \in U : u^{-1} \in U$
• die von Elementen erzeugten Untergruppen:
  • sei (G, \cdot)$(G, \cdot)$ eine Gruppe, dann gilt \lang a \rang = \{a^k|k\in \Z\} \leq G$\lang a \rang = \{a^k|k\in \Z\} \leq G$
    • anders: \lang a \rang = \{e, a, a^2, ..., a^{n-1}\}$\lang a \rang = \{e, a, a^2, ..., a^{n-1}\}$
    • \lang a \rang \subseteq G$\lang a \rang \subseteq G$
    • e \in \lang a \rang: e = a^0$e \in \lang a \rang: e = a^0$
    • a^k, a^l \in \lang a \rang \implies a^ka^l = a^{k+l} \in \lang a \rang$a^k, a^l \in \lang a \rang \implies a^ka^l = a^{k+l} \in \lang a \rang$
    • \forall \; a^k \; \exists \; a^{-k}: a^ka^{-k} = a^{k-k} = a^0 = e$\forall \; a^k \; \exists \; a^{-k}: a^ka^{-k} = a^{k-k} = a^0 = e$
  • Ordnung eines Elements a \in G$a \in G$: |\lang a \rang| = O(a)$|\lang a \rang| = O(a)$
    • O(a) = n$O(a) = n$, wenn |\lang a \rang| = n \in \N$|\lang a \rang| = n \in \N$, sonst \infty$\infty$
    • anders: |\lang a \rang| = |\{e,a^1,...,a^{n-1}\}| = n$|\lang a \rang| = |\{e,a^1,...,a^{n-1}\}| = n$ mit n$n$ als kleinste natürliche Zahl wofür a^n = e$a^n = e$
    • Satz über die Ordnung von Gruppenelementen: für eine Gruppe G$G$ mit neutralem Element e$e$ gilt für ein beliebiges Element a$a$...
      • wenn O(a) = \infty$O(a) = \infty$, dann gilt a^i \neq a^j \;\forall i \neq j$a^i \neq a^j \;\forall i \neq j$
      • wenn O(a) \in \N$O(a) \in \N$, so gilt O(a) = n$O(a) = n$ mit n$n$ als kleinste natürliche Zahl wofür a^n = e$a^n = e$
    • Ordnung bestimmen: multipliziere x$x$ mit sich selbst, bis e$e$ erreicht wird, die Potenz ist dann die Gruppenordnung
• Satz von Lagrange: |U|$|U|$ teilt |G|$|G|$ (|U|$|U|$ ist ein Teiler von |G|$|G|$, bzw. |G|$|G|$ ist ein Vielfaches von |U|$|U|$, bzw. \exists n \in \N: |U| * n = |G|$\exists n \in \N: |U| * n = |G|$)
• Satz von Euler: \forall a \in G: a^{|G|} = e$\forall a \in G: a^{|G|} = e$

Ringe

• eine Menge R$R$ mit zwei Verknüpfungen +, \cdot$+, \cdot$ heißt Ring, falls folgendes gilt:
  1. (R, +)$(R, +)$ ist eine abelsche Gruppe
  2. Multiplikation ist abgeschlossen: \forall a,b \in R: a \cdot b \in R$\forall a,b \in R: a \cdot b \in R$
  3. Multiplikation ist assoziativ: \forall a,b,c \in R:a(bc) = (ab)c \in R$\forall a,b,c \in R:a(bc) = (ab)c \in R$
  4. Distributivgesetze: \forall a,b,c \in R$\forall a,b,c \in R$ gilt...
     4.1: (a+b)c = ac + bc$(a+b)c = ac + bc$
     4.2: a(b+c) = ab + ac$a(b+c) = ab + ac$
• R$R$ ist kommutativ, wenn \forall a,b\in R:ab = ba$\forall a,b\in R:ab = ba$
• R$R$ ist ein Ring mit Einselement, falls \forall a \in R \; \exists e : ae = a = ea$\forall a \in R \; \exists e : ae = a = ea$
• Beispiele:
  • (\Z, +, \cdot)$(\Z, +, \cdot)$: kommutativer Ring mit Einselement 1
  • (\R, +, \cdot)$(\R, +, \cdot)$: kommutativer Ring mit Einselement 1
  • (\mathbb{C}, +, \cdot)$(\mathbb{C}, +, \cdot)$: kommutativer Ring mit Einselement 1
  • (K^{n \times n}, +, \cdot)$(K^{n \times n}, +, \cdot)$: nicht kommutativer Ring mit Einselement E_n$E_n$
  • (\Z_n, +, \cdot)$(\Z_n, +, \cdot)$: kommutativer Ring mit Einselement \overline1$\overline1$
• Einheitengruppe eines Rings mit Einselement:
  • sei (R,+,\cdot)$(R,+,\cdot)$ ein Ring mit Einselement 1, dann ist die Einheitengruppe R^\times = \{a\in R | \exists b \in R: ab = 1 = ba\}$R^\times = \{a\in R | \exists b \in R: ab = 1 = ba\}$ die Menge aller multiplikativ invertierbaren Elemente
  • \mathbb{Q}^\times = \mathbb{Q} \backslash \{0\}$\mathbb{Q}^\times = \mathbb{Q} \backslash \{0\}$, \mathbb{R}^\times = \mathbb{R} \backslash \{0\}$\mathbb{R}^\times = \mathbb{R} \backslash \{0\}$, \mathbb{C}^\times = \mathbb{C} \backslash \{0\}$\mathbb{C}^\times = \mathbb{C} \backslash \{0\}$
  • z.B. \Z_6^\times = \{\overline 1, \overline 5\}$\Z_6^\times = \{\overline 1, \overline 5\}$
    • wenn das Produkt zweier Faktoren \overline 0$\overline 0$ ist, ist keiner dieser Faktoren invertierbar: \overline 2 * \overline 3 = \overline 0$\overline 2 * \overline 3 = \overline 0$, \overline 4 * \overline 3 = \overline 0$\overline 4 * \overline 3 = \overline 0$

Vektorräume

Körper

• ein Ring (K, +, \cdot)$(K, +, \cdot)$ mit Einselement 1 heißt Körper, falls folgendes gilt:
  1. (K, +)$(K, +)$ abelsche Gruppe (neutrales Element 0)
  2. (K \backslash \{0\}, \cdot)$(K \backslash \{0\}, \cdot)$ abelsche Gruppe (neutrales Element 1)
  3. Distributivgesetze: \forall a,b,c\in K: a(b+c) = ab + ac \land (a+b)c = ac+ bc$\forall a,b,c\in K: a(b+c) = ab + ac \land (a+b)c = ac+ bc$
• Beispiele: (\mathbb{Q}, +, \cdot)$(\mathbb{Q}, +, \cdot)$, (\mathbb{R}, +, \cdot)$(\mathbb{R}, +, \cdot)$, (\mathbb{C}, +, \cdot)$(\mathbb{C}, +, \cdot)$, \Z / p\Z$\Z / p\Z$

Vektorräume

• K$K$ sei ein Körper, dann heißt V$V$ ein K$K$-Vektorraum (über K$K$), falls folgendes gilt:
  1. (V, +)$(V, +)$ ist eine abelsche Gruppe
  2. \forall u,v \in V, \forall \lambda, \mu \in K:$\forall u,v \in V, \forall \lambda, \mu \in K:$
     2.1. Distributivität I: \lambda(u + v) = \lambda u + \lambda v$\lambda(u + v) = \lambda u + \lambda v$
     2.2. Distributivität II: (\lambda + \mu) v = \lambda v + \mu v$(\lambda + \mu) v = \lambda v + \mu v$
     2.3. Assoziativität: (\lambda \mu) v = \lambda (\mu v)$(\lambda \mu) v = \lambda (\mu v)$
     2.4. neutrales Element: 1 v = v$1 v = v$ für 1 \in K$1 \in K$
• Beispiele:
  • K^n$K^n$ (Vektoren)
  • K^{m\times n}$K^{m\times n}$ (Vektorraum der Matrizen)
  • K[x] := \{ a_0 + a_1 x + a_2 x^2 + ... + a_n x^n | a_i \in K, n \in N\} = \sum_{i=0}^na_i x^i$K[x] := \{ a_0 + a_1 x + a_2 x^2 + ... + a_n x^n | a_i \in K, n \in N\} = \sum_{i=0}^na_i x^i$ (Vektorraum der Polynome für eine Variable x$x$)
• Regeln:
  • 0 * v = 0$0 * v = 0$ (Nullskalar * v \in V$v \in V$ = Nullvektor)
  • \lambda * 0 = 0$\lambda * 0 = 0$ (Skalar * Nullvektor = Nullvektor)
  • \lambda * v = 0 \Leftrightarrow \lambda = 0 \; \lor \; v = 0$\lambda * v = 0 \Leftrightarrow \lambda = 0 \; \lor \; v = 0$
• Untervektorräume:
  • REZEPT: eine Teilmenge U \subseteq V$U \subseteq V$, wobei V$V$ ein K-Vektorraum ist, heißt Untervektorraum / Unterraum von V$V$ (geschrieben U \leq V$U \leq V$), wenn folgendes gilt:
    1. Teilmengenbeziehung: U \subseteq V$U \subseteq V$ (impl.)
    2. neutrales Element: 0 \in U$0 \in U$
    3. Abgeschlossenheit: u,v \in U \implies u + v \in U$u,v \in U \implies u + v \in U$
    4. \lambda \in K, u \in U \implies \lambda u \in U$\lambda \in K, u \in U \implies \lambda u \in U$
  • wenn U, W \leq V$U, W \leq V$, dann U \cap W \leq V$U \cap W \leq V$

Basen von Vektorräumen

• ist V$V$ ein K$K$-Vektorraum, so nennt man B \subseteq V$B \subseteq V$ eine Basis von V$V$, falls folgendes gilt:
  • B$B$ ist linear unabhängig
  • B$B$ erzeugt V$V$
• Beispiel:
  • E_n = \left\{\begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}, ..., \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix}\right\} \subseteq \R^n$E_n = \left\{\begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}, ..., \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix}\right\} \subseteq \R^n$, linear unabhängig, x_1\begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}+...+x_n \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix} = \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{pmatrix}$x_1\begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}+...+x_n \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix} = \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{pmatrix}$
• Regeln:
  • jeder Vektorraum hat eine Basis
  • B \subseteq V$B \subseteq V$ Basis von V$V$ \Longleftrightarrow$\Longleftrightarrow$ B$B$ ist ein minimales Erzeugendensystem von V$V$ \Longleftrightarrow$\Longleftrightarrow$ B$B$ ist eine maximale linear unabhängige Teilmenge von V$V$
  • jede linear unabhängige Teilmenge von V$V$ kann man zu einer Basis ergänzen
  • jedes Erzeugendensystem von V$V$ kann man zu einer Basis verkürzen
  • ist B$B$ eine Basis von V$V$, so kann man jedes v \in V$v \in V$ auf genau eine Weise bezüglich B$B$ darstellen als Linearkombination (v = \lambda_1 b_1 + ... + \lambda_n b_n$v = \lambda_1 b_1 + ... + \lambda_n b_n$)
  • je zwei Basen B_1, B_2$B_1, B_2$ von V$V$ haben die gleiche Mächtigkeit |B_1| = |B_2|$|B_1| = |B_2|$
  • Dimension \dim(v) = |B|$\dim(v) = |B|$: Mächtigkeit einer (jeder) Basis B$B$ von V$V$
    • \dim(\R^n) = n, \dim(K^{m\times n}) = m*n, \dim(K[x]) = \infty, \dim(\R^\R) = \infty, \dim(\R[x]_n) = n + 1$\dim(\R^n) = n, \dim(K^{m\times n}) = m*n, \dim(K[x]) = \infty, \dim(\R^\R) = \infty, \dim(\R[x]_n) = n + 1$
  • ist V$V$ ein K$K$-Vektorraum der Dimension n \in \N$n \in \N$, dann gilt:
    • jede linear unabhängige Menge mit n$n$ Elementen ist eine Basis
    • jedes Erzeugendensystem von V$V$ mit n$n$ Elementen ist eine Basis
    • jede Menge mit mehr als n$n$ Vektoren ist stets linear abhängig
• REZEPT: Basis aus Menge von Vektoren anzugeben (Beispiel):
  • gegeben: \left\{\begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} -1\\ 1\\ 0 \end{pmatrix}, \begin{pmatrix} -1\\ 3\\ 2 \end{pmatrix}\right\}$\left\{\begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} -1\\ 1\\ 0 \end{pmatrix}, \begin{pmatrix} -1\\ 3\\ 2 \end{pmatrix}\right\}$
  • LGS: \begin{pmatrix} 1 & 1 & 2 \\ -1& 1 & 0 \\ -1& 3 & 2 \\ \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 2 \\ 0& 1 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix} \to$\begin{pmatrix} 1 & 1 & 2 \\ -1& 1 & 0 \\ -1& 3 & 2 \\ \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 2 \\ 0& 1 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix} \to$ Basis: \lang \begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} \rang$\lang \begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} \rang$ (Vektoren, außer Nullzeile) \to$\to$ ergänzt: \lang \begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix}, \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \rang$\lang \begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}, \begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix}, \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \rang$ (Zeilenstufenform)

Linearkombinationen

• Vektor, der sich durch gegebene Vektoren unter Verwendung der Vektoraddition und der skalaren Multiplikation ausdrücken lässt
  • z.B. v_1 = \begin{pmatrix} 1\\ 1 \end{pmatrix}, v_2 = \begin{pmatrix} 2\\ -1 \end{pmatrix}, v = \begin{pmatrix} 4\\ 1 \end{pmatrix}$v_1 = \begin{pmatrix} 1\\ 1 \end{pmatrix}, v_2 = \begin{pmatrix} 2\\ -1 \end{pmatrix}, v = \begin{pmatrix} 4\\ 1 \end{pmatrix}$
    • \begin{pmatrix} 1 & 2 & 4\\ 1 & -1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 2 & 4\\ 0 & -3 & 3 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 2\\ 0 & 1 & 1 \end{pmatrix} \to \lambda_1 =2, \lambda_2 = 1$\begin{pmatrix} 1 & 2 & 4\\ 1 & -1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 2 & 4\\ 0 & -3 & 3 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 2\\ 0 & 1 & 1 \end{pmatrix} \to \lambda_1 =2, \lambda_2 = 1$
    • selbe Regeln wie bei LGS: \begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix} \to \infty$\begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix} \to \infty$ Lösungen
  • z.B. \R[x]$\R[x]$ (Polynome), p_1 = x + 1$p_1 = x + 1$, p_2 = x - 1$p_2 = x - 1$, p = 2x+1$p = 2x+1$
    • \lambda_1 (x+1) + \lambda_2 (x-1) = 2x + 1 \to (\lambda_1 + \lambda_2) x + (\lambda_1 - \lambda_2) = 2x+1$\lambda_1 (x+1) + \lambda_2 (x-1) = 2x + 1 \to (\lambda_1 + \lambda_2) x + (\lambda_1 - \lambda_2) = 2x+1$
    • Polynome sind gleich, wenn die Koeffizienten gleich sind: \lambda_1 + \lambda_2 = 2$\lambda_1 + \lambda_2 = 2$, \lambda_1 - \lambda_2 = 1$\lambda_1 - \lambda_2 = 1$
    • \begin{pmatrix} 1 & 1 & 2\\ 1 & -1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 2\\ 0 & -2 & -1 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 1.5\\ 0 & 1 & 0.5 \end{pmatrix} \to \lambda_1 = 1.5, \lambda_2 = 0.5$\begin{pmatrix} 1 & 1 & 2\\ 1 & -1 & 1 \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 2\\ 0 & -2 & -1 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 1.5\\ 0 & 1 & 0.5 \end{pmatrix} \to \lambda_1 = 1.5, \lambda_2 = 0.5$
  • \nexists \lambda_1, \lambda_2: \exp = \lambda_1 \sin + \lambda_2 \cos$\nexists \lambda_1, \lambda_2: \exp = \lambda_1 \sin + \lambda_2 \cos$
• Erzeugnis von X$X$:
  • sei V$V$ ein K-Vektorraum mit X \subseteq V, X \neq \emptyset$X \subseteq V, X \neq \emptyset$, dann gilt \lang x \rang = lin(x) = span(x) = \{\sum_{i=1}^n \lambda_iv^i | v_i \in X, \lambda_i \in K, n \in \N\}$\lang x \rang = lin(x) = span(x) = \{\sum_{i=1}^n \lambda_iv^i | v_i \in X, \lambda_i \in K, n \in \N\}$ (alle Linearkombinationen von Elementen aus X$X$)
    • \lang x \rang \leq V$\lang x \rang \leq V$
    • x \subseteq \lang x \rang$x \subseteq \lang x \rang$
    • \lang x \rang = \bigcap_{x \leq U \leq V} U$\lang x \rang = \bigcap_{x \leq U \leq V} U$
    • \lang \emptyset \rang = \{0\}$\lang \emptyset \rang = \{0\}$
  • z.B. \R^n = \lang \begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}, ..., \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix} \rang$\R^n = \lang \begin{pmatrix} 1\\ 0\\ \vdots\\ 0 \end{pmatrix}, ..., \begin{pmatrix} 0\\ 0\\ \vdots\\ 1 \end{pmatrix} \rang$; \R[x] =\lang 1,x,x^2,... \rang$\R[x] =\lang 1,x,x^2,... \rang$
• REZEPT: Darstellen eines Vektors als Linearkombination:
  • mache den Ansatz \lambda_1 v_1 + ... + \lambda_n v_n = v$\lambda_1 v_1 + ... + \lambda_n v_n = v$ in den Unbestimmten \lambda_1, ... ,\lambda_n$\lambda_1, ... ,\lambda_n$
    • im Fall V = K^n$V = K^n$ liefert dies ein LGS
    • im Fall V = K^{m \times n}$V = K^{m \times n}$ liefert dies einen Koeffizientenvergleich von Matrizen
    • im Fall V = K[x]$V = K[x]$ liefert dies einen Koeffizientenvergleich von Polynomen
    • im Fall V = K^M$V = K^M$ liefert dies einen Wertevergleich von Funktionen
  • wenn die Gleichung eine Lösung hat, so ist v$v$ eine Linearkombination
    • wenn nicht, so ist v$v$ keine Linearkombination und breche ab
  • löse das Gleichungssystem

Lineare Unabhängigkeit

• eine Familie von Vektoren eines Vektorraums heißt linear unabhängig, wenn sich der Nullvektor nur durch eine Linearkombination der Vektoren erzeugen lässt, in der alle Koeffizienten der Kombination auf den Wert null gesetzt werden

  • anders: keiner der Vektoren lässt sich als Linearkombination der anderen Vektoren der Familie darstellen

• REZEPT: Bestimmen, ob n$n$ Vektoren linear unabhängig sind:

  • \lambda_1 v_1 + ... + \lambda_n v_n = 0$\lambda_1 v_1 + ... + \lambda_n v_n = 0$
  • mittels LGS (Gauß-Algorithmus) lösen
    • \exists!$\exists!$ die Nulllösung \forall i : \lambda_i = 0 \to v_1, ... v_n$\forall i : \lambda_i = 0 \to v_1, ... v_n$ linear unabhängig (homogenes LGS)
    • \exists$\exists$ mindestens eine Lösung, wofür \lambda_i \neq 0 \to v_1, ... v_n$\lambda_i \neq 0 \to v_1, ... v_n$ linear abhängig

• REZEPT: Bestimmen einer Basis aus einem Erzeugendensystem

  • gegeben: Erzeugendensystem X$X$ eines Vektorraums V$V$
    • prüfe, ob X$X$ linear unabhängig ist
      1. wenn ja, dann ist X$X$ eine Basis
      2. wenn nicht, dann entferne aus X$X$ Elemente a_1, ... , a_r$a_1, ... , a_r$, die Linearkombinationen anderer Elemente aus X$X$ sind und beginne mit \~{X}$\~{X}$ erneut
  • gegeben: linear unabhängige Teilmenge X$X$ eines Vektorraums V$V$
    • prüfe, ob X$X$ ein Erzeugendensystem von V$V$ ist
      1. wenn ja, dann ist X$X$ eine Basis
      2. wenn nicht, dann wähle aus V$V$ Elemente a_1, ... , a_r$a_1, ... , a_r$, so dass \~{X} = X \cup \{a_1, ... , a_r\}$\~{X} = X \cup \{a_1, ... , a_r\}$ linear unabhängig ist und beginne mit \~{X}$\~{X}$ erneut
  • Durchführen bei Spaltenvektoren X = \{v_1, ..., v_s\}, v_i \in \mathbb{K}^n$X = \{v_1, ..., v_s\}, v_i \in \mathbb{K}^n$: (p. 153)
    • schreibe Spalten v_i$v_i$ als Zeilen v_i^T$v_i^T$ und wende elementare Zeilenumformungen an
    • die Transponierten der ersten r$r$ Zeilen bilden eine Basis B = \{b_1, ... , b_r\}$B = \{b_1, ... , b_r\}$ von \langle X\rangle$\langle X\rangle$
    • ergänzt man die Matrix durch n-r$n-r$ weitere Zeilen, die die Zeilenstufenform fortsetzen, verlängert man die linear unabhängige Menge zu einer Basis

Orthogonalität

Skalarprodukt

• eine Abbildung s : (v,w) \to s(v,w)$s : (v,w) \to s(v,w)$ (Skalarprodukt (v,w) \to \langle v,w \rangle$(v,w) \to \langle v,w \rangle$) ist...
  • bilinear, wenn für alle v, v', w, w' \in V$v, v', w, w' \in V$ und \lambda \in \R$\lambda \in \R$ gilt:
    • \langle \lambda v + v', w \rangle = \lambda \langle v,w \rangle + \langle v', w \rangle$\langle \lambda v + v', w \rangle = \lambda \langle v,w \rangle + \langle v', w \rangle$ (Linearität im I. Argument)
    • \langle v, \lambda w + w' \rangle = \lambda \langle v,w \rangle + \langle v, w'\rangle$\langle v, \lambda w + w' \rangle = \lambda \langle v,w \rangle + \langle v, w'\rangle$ (Linearität im II. Argument)
  • symmetrisch, wenn: \langle v,w \rangle = \langle w,v \rangle$\langle v,w \rangle = \langle w,v \rangle$
  • positiv definit, wenn \langle v,v \rangle \geq 0$\langle v,v \rangle \geq 0$ und \langle v,v \rangle = 0 \iff v = 0$\langle v,v \rangle = 0 \iff v = 0$
• Satz: eine Abbildung ist ein Skalarprodukt, wenn Linearität im I. Argument, Symmetrie und positive Definitheit gelten
• Standardskalarprodukt / kanonisches Skalarprodukt:
  • \langle v, w \rangle := v^Tw = \sum_{i = 1}^n v_iw_i$\langle v, w \rangle := v^Tw = \sum_{i = 1}^n v_iw_i$
  • für A \in R^{n \times n}, A = A^T, A$A \in R^{n \times n}, A = A^T, A$ positiv definit (quadratisch, symmetrisch, pos. def.) gilt \langle v, w \rangle_A := v^TAw$\langle v, w \rangle_A := v^TAw$
• für alle v,w \in V$v,w \in V$ gilt \lang 0, w\rang = 0 = \lang v, 0 \rang$\lang 0, w\rang = 0 = \lang v, 0 \rang$

Länge, Abstand, Winkel, Orthogonalität

• Länge / Norm eines Vektors: ||v|| = \sqrt{\langle v, v \rangle}$||v|| = \sqrt{\langle v, v \rangle}$
  • euklidische Norm: Norm mit kanonischem Skalarprodukt
  • z.B. \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \to \text{mit SSP} = \sqrt{14}$\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \to \text{mit SSP} = \sqrt{14}$
• Abstand von zwei Vektoren v$v$ und w$w$: d(v,w) = || v - w || = || w - v ||$d(v,w) = || v - w || = || w - v ||$
• Winkel zwischen zwei nicht-nullen Vektoren v$v$ und w$w$: \angle(v,w) = \arccos \left( \frac{\langle v, w \rangle}{||v||||w||} \right)$\angle(v,w) = \arccos \left( \frac{\langle v, w \rangle}{||v||||w||} \right)$
• v$v$ und w$w$ sind senkrecht / orthogonal (v \perp w$v \perp w$), wenn \langle v, w \rangle = 0$\langle v, w \rangle = 0$

Orthogonalsystem, -basis; Orthonormalsystem, -basis

• Orthogonalsystem (OGS): B \subseteq V$B \subseteq V$, für alle v, w \in B$v, w \in B$ mit v \neq w$v \neq w$ gilt v \perp w$v \perp w$
• Orthogonalbasis (OGB): B \subseteq V$B \subseteq V$, B$B$ ist Orthogonalsystem und Basis
• Orthonormalsystem (ONS): B \subseteq V$B \subseteq V$, B$B$ ist Orthogonalsystem und ||v|| = 1$||v|| = 1$ für alle v$v$ (normierte Vektoren)
• Orthonormalbasis (ONB): B \subseteq V$B \subseteq V$, B$B$ ist Orthonormalsystem und Basis

Normieren eines Vektors

• ersetze jedes v \neq 0$v \neq 0$ durch \^{v} := \frac{1}{||v||}v$\^{v} := \frac{1}{||v||}v$, um ein Orthogonalsystem in ein Orthonormalsystem umzuwandeln
  • durch Normieren einer Orthogonalbasis B$B$ erhält man eine Orthonormalbasis \~{B}$\~{B}$
  • E_n = \{e_1, ... , e_n \}$E_n = \{e_1, ... , e_n \}$ ist eine Orthonormalbasis des \R^n$\R^n$
  • mit dem Kronecker-Delta: B$B$ ist ONB \iff$\iff$ \forall i, j : \langle b_i, b_j \rangle = \delta_{ij}$\forall i, j : \langle b_i, b_j \rangle = \delta_{ij}$

Orthogonale Zerlegung von v längs a (p. 167)

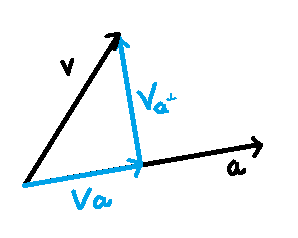
• v = v_a + v_{a^\perp}$v = v_a + v_{a^\perp}$ mit v_a = \lambda a$v_a = \lambda a$ und v_{a^\perp} \perp a$v_{a^\perp} \perp a$
• erhalte Zerlegung wie folgt:
  1. v_a = \frac{\langle v,a \rangle}{\langle a,a \rangle}a$v_a = \frac{\langle v,a \rangle}{\langle a,a \rangle}a$
  2. v_{a^\perp} = v - v_a$v_{a^\perp} = v - v_a$
• REZEPT: Bestimmen der Linearkombination bezüglich einer ONB:
  • sei v = \lambda_1 b_1 + ... + \lambda_n b_n$v = \lambda_1 b_1 + ... + \lambda_n b_n$ für jedes v \in V$v \in V$ bezüglich der ONB B = \{b_1,..., b_n\}$B = \{b_1,..., b_n\}$
  • dann findet man die Linearkombination für jedes v$v$ wie folgt: \lambda_i = \langle v, b_i \rangle$\lambda_i = \langle v, b_i \rangle$
    • z.B. v = \begin{pmatrix} 3 \\ 2 \end{pmatrix}$v = \begin{pmatrix} 3 \\ 2 \end{pmatrix}$ bzgl. b_1 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix}$b_1 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix}$ und b_2 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix}$b_2 = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix}$
    • \lambda_1 = \langle (3,2)^T, b_1 \rangle = \frac{5}{\sqrt2}$\lambda_1 = \langle (3,2)^T, b_1 \rangle = \frac{5}{\sqrt2}$
    • \lambda_2 = \langle (3,2)^T, b_2 \rangle = \frac{1}{\sqrt2}$\lambda_2 = \langle (3,2)^T, b_2 \rangle = \frac{1}{\sqrt2}$
    • folgt: v = \frac{5}{\sqrt2}b_1 + \frac{1}{\sqrt2}b_2$v = \frac{5}{\sqrt2}b_1 + \frac{1}{\sqrt2}b_2$

Gram-Schmidt Orthonormierungsverfahren

• gegeben: Basis B = \{a_1, ... , a_n\}$B = \{a_1, ... , a_n\}$
• gesucht: ONB
• Verfahren: bilde Vektoren b_1, ... , b_n$b_1, ... , b_n$ wie folgt:
  1. b_1 = \frac{1}{||a_1||}a_1$b_1 = \frac{1}{||a_1||}a_1$
  2. b_2 = \frac{1}{||c_2||}c_2$b_2 = \frac{1}{||c_2||}c_2$ mit c_2 = a_2 - \langle a_2, b_1 \rangle b_1$c_2 = a_2 - \langle a_2, b_1 \rangle b_1$
  3. b_3 = \frac{1}{||c_3||}c_3$b_3 = \frac{1}{||c_3||}c_3$ mit c_3 = a_3 - \langle a_3, b_1 \rangle b_1 - \langle a_3, b_2 \rangle b_2$c_3 = a_3 - \langle a_3, b_1 \rangle b_1 - \langle a_3, b_2 \rangle b_2$
     ...
• allgemein: b_n = \frac{1}{||c_n||}c_n$b_n = \frac{1}{||c_n||}c_n$ mit c_n = a_n - \langle a_n, b_1 \rangle b_1 - ... - \langle a_n, b_{n-1} \rangle b_{n-1}$c_n = a_n - \langle a_n, b_1 \rangle b_1 - ... - \langle a_n, b_{n-1} \rangle b_{n-1}$
  • anders: b_{k+1} = \frac{1}{||c_{k+1}||}c_{k+1}$b_{k+1} = \frac{1}{||c_{k+1}||}c_{k+1}$ mit c_{k+1} = a_{k+1} - \sum_{i = 1}^k \langle a_{k+1}, b_i \rangle b_i$c_{k+1} = a_{k+1} - \sum_{i = 1}^k \langle a_{k+1}, b_i \rangle b_i$

Die orthogonale Projektion

• das orthogonale Komplement: U^\perp = \{v \in V \; | \; v \perp u \; \forall u \in U \}$U^\perp = \{v \in V \; | \; v \perp u \; \forall u \in U \}$
  • U^\perp$U^\perp$ ist Untervektorraum von V$V$
  • U^\perp \cap U = \{0\}$U^\perp \cap U = \{0\}$
  • jedes v \in V$v \in V$ hat genau eine Darstellung der Form v = u + u^\perp$v = u + u^\perp$ mit u \in U, u^\perp \in U^\perp$u \in U, u^\perp \in U^\perp$
  • wenn \dim(V) = n$\dim(V) = n$, dann \dim(U^\perp) = n - \dim(U)$\dim(U^\perp) = n - \dim(U)$
• REZEPT: Bestimmen des orthogonalen Komplements:
  • bestimme eine Basis \{b_1, ..., b_r\}$\{b_1, ..., b_r\}$ von U$U$ mit \dim(V) = n$\dim(V) = n$ und \dim(U) = r$\dim(U) = r$
  • bestimme n-r$n-r$ linear unabhängige Vektoren a_1, ... , a_{n-r}$a_1, ... , a_{n-r}$, die zu allen b_1, ... , b_r$b_1, ... , b_r$ orthogonal sind
  • U^\perp = \langle a_1, ... , a_{n-r} \rangle$U^\perp = \langle a_1, ... , a_{n-r} \rangle$
• die orthogonale Projektion: p_U : v = u + u^\perp \to u$p_U : v = u + u^\perp \to u$
  • der minimale Abstand von v$v$ zu U$U$: || u^\perp || = || v - u ||$|| u^\perp || = || v - u ||$
  • u$u$ als Lösung der Minimierungsaufgabe: || v - u || = \min$|| v - u || = \min$
• REZEPT: die Minimierungsaufgabe:
  • wähle Basis \{b_1, ... , b_r \}$\{b_1, ... , b_r \}$ von U$U$
  • setze u = Ax$u = Ax$ mit A = (b_1, ... b_r) \in \R^{n \times r}$A = (b_1, ... b_r) \in \R^{n \times r}$ für x = (\lambda_1, ... ,\lambda_r)^T \in R^r$x = (\lambda_1, ... ,\lambda_r)^T \in R^r$
  • bestimme x \in R^r$x \in R^r$ mit || v - Ax || = \min$|| v - Ax || = \min$

Das lineare Ausgleichsproblem

• suche ein x$x$, sodass zu einem Vektor v$v$ und einer Matrix A$A$ der Wert ||v-Ax||$||v-Ax||$ minimal wird
• REZEPT:: x \in \R^r$x \in \R^r$ mit A^TAx = A^Tv$A^TAx = A^Tv$
  • genau dann eindeutig lösbar, wenn rg(A) = r$rg(A) = r$ (Rang von A$A$ maximal) ist
  • Beispiel:
    • v = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$v = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$, U = \langle \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \rangle$U = \langle \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \rangle$
    • dann A = \begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 1 \end{pmatrix}$A = \begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 1 \end{pmatrix}$
    • A^TA = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 2 \\ 2 & 3 \end{pmatrix}$A^TA = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 2 \\ 2 & 3 \end{pmatrix}$
    • A^Tv = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 4 \\ 6 \end{pmatrix}$A^Tv = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 4 \\ 6 \end{pmatrix}$
    • LGS (A^TAx \; | \; A^Tv$A^TAx \; | \; A^Tv$): \begin{pmatrix} 2 & 2 & 4 \\ 2 & 3 & 6 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \end{pmatrix} \to \lambda_1 = 0, \lambda_2 = 2$\begin{pmatrix} 2 & 2 & 4 \\ 2 & 3 & 6 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \end{pmatrix} \to \lambda_1 = 0, \lambda_2 = 2$
    • dann u = \lambda_1b_1 + \lambda_2b_2 = 0b_1 + 2b_2 = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix}$u = \lambda_1b_1 + \lambda_2b_2 = 0b_1 + 2b_2 = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix}$
    • minimaler Abstand: u^\perp = (-1, 0, 1)^T \to ||u^\perp|| = \sqrt{2}$u^\perp = (-1, 0, 1)^T \to ||u^\perp|| = \sqrt{2}$
• Bemerkung: wenn B$B$ eine ONB von U$U$ ist, gilt x = A^Tv$x = A^Tv$
• REZEPT für überbestimmte LGS: nutze A^TAx = A^Tv$A^TAx = A^Tv$
• REZEPT - die Methode der kleinsten Quadrate:
  • gegeben: Stützstellen (t_1, y_1), ... , (t_n, y_n)$(t_1, y_1), ... , (t_n, y_n)$
  • gesucht:
    • Ausgleichsgerade f(x) = \lambda_1 + \lambda_2x$f(x) = \lambda_1 + \lambda_2x$
      • d.h. f_1(x) = 1$f_1(x) = 1$, f_2(x)=x$f_2(x)=x$
    • Ausgleichsparabel g(x) = \mu_1 + \mu_2x + \mu_3x^2$g(x) = \mu_1 + \mu_2x + \mu_3x^2$
      • d.h. g_1(x) = 1$g_1(x) = 1$, g_2(x)=x$g_2(x)=x$, g_3(x)=x^2$g_3(x)=x^2$
  • Lösung:
    • setze v = (y_1, ... , y_n)^T$v = (y_1, ... , y_n)^T$ und A=\begin{pmatrix} f_1(t_1) & \dots & f_r(t_1) \\ \vdots & \ddots & \vdots \\ f_1(t_n) & \dots & f_r(t_n) \end{pmatrix}$A=\begin{pmatrix} f_1(t_1) & \dots & f_r(t_1) \\ \vdots & \ddots & \vdots \\ f_1(t_n) & \dots & f_r(t_n) \end{pmatrix}$
    • löse A^TAx = A^Tv$A^TAx = A^Tv$ und erhalte x = (\lambda_1, ... , \lambda_r)^T$x = (\lambda_1, ... , \lambda_r)^T$
    • die Ausgleichsfunktion ist f = \lambda_1 f_1 + ... + \lambda_r f_r$f = \lambda_1 f_1 + ... + \lambda_r f_r$

Lineare Abbildungen

• eine Abbildung heißt linear oder Homomorphismus, falls f(\lambda v + w) = \lambda f(v) + f(w)$f(\lambda v + w) = \lambda f(v) + f(w)$
• Eigenschaften:
  • f(0_V) = 0_W$f(0_V) = 0_W$
  • sind f : V \to W$f : V \to W$ und g : W \to U$g : W \to U$ linear, so ist auch g \circ f : V \to U$g \circ f : V \to U$ linear
  • ist f : V \to W$f : V \to W$ bijektiv und linear, so ist auch f^{-1} : W \to V$f^{-1} : W \to V$ bijektiv und linear
• REZEPT: Test, ob f$f$ linear ist oder nicht:
  • gilt f(0) = 0$f(0) = 0$?
    • wenn nicht, dann ist f$f$ nicht linear, sonst...
  • zeige, dass f(\lambda v + w) = \lambda f(v) + f(w)$f(\lambda v + w) = \lambda f(v) + f(w)$
    • anders: f(v +w) = f(v) + f(w)$f(v +w) = f(v) + f(w)$ und dann f(\lambda v) = \lambda f(v)$f(\lambda v) = \lambda f(v)$
  • andersrum, finde ein Gegenbeispiel

Bild, Kern, Dimensionsformel

• ist f : V \to W$f : V \to W$ linear, so sind \ker$\ker$ und \text{Bild}$\text{Bild}$ Untervektorräume von V$V$ bzw. W$W$:
  • \ker(f) = f^{-1}(\{0\}) = \{v \in V \; | \; f(v) = 0 \} \subseteq V$\ker(f) = f^{-1}(\{0\}) = \{v \in V \; | \; f(v) = 0 \} \subseteq V$
  • \text{Bild}(f) = f(V) = \{f(v) \; | \; v \in V\} \subseteq W$\text{Bild}(f) = f(V) = \{f(v) \; | \; v \in V\} \subseteq W$
• Defekt von f$f$: \text{def}(f) = \dim(\ker(f))$\text{def}(f) = \dim(\ker(f))$
  • f$f$ ist genau dann injektiv, wenn \ker(f) = \{0\}$\ker(f) = \{0\}$ bzw. \text{def}(f) = 0$\text{def}(f) = 0$
• Rang von f$f$: \text{rg}(f) = \dim(\text{Bild}(f))$\text{rg}(f) = \dim(\text{Bild}(f))$
• Dimensionsformel: \dim(V) = \dim(\ker(f)) + \dim(\text{Bild}(f))$\dim(V) = \dim(\ker(f)) + \dim(\text{Bild}(f))$
  • wenn \dim(V) = \dim(W)$\dim(V) = \dim(W)$, dann ist f$f$ bijektiv

Koordinatenvektoren

• gegeben: geordnete Basis B = (b_1, ..., b_n)$B = (b_1, ..., b_n)$
• so kann man jeden Vektor v$v$ eindeutig als Linearkombination bzgl. B$B$ darstellen
  • v = \lambda_1b_1 + ... + \lambda_nb_n$v = \lambda_1b_1 + ... + \lambda_nb_n$
• Koordinatenvektor von v$v$ bzgl. B$B$: _Bv = (\lambda_1, ... , \lambda_n)^T$_Bv = (\lambda_1, ... , \lambda_n)^T$
  • es gilt _B(\lambda v + w) = \lambda_B v + _B w$_B(\lambda v + w) = \lambda_B v + _B w$, d.h. die bijektive Abbildung _B : v \to _Bv$_B : v \to _Bv$ ist linear

Restklassen, Modulorechnen

• a \mod n := r$a \mod n := r$ mit r \in \{0, ..., n-1\}$r \in \{0, ..., n-1\}$ und a = k \cdot n + r$a = k \cdot n + r$
  • a = 16, n = 7 \to 16 \mod 7 = 2$a = 16, n = 7 \to 16 \mod 7 = 2$
  • a = -16, n = 7 \to -16 \mod 7 = 5$a = -16, n = 7 \to -16 \mod 7 = 5$ (alt. -2 \to 7 - 2 \to 5$-2 \to 7 - 2 \to 5$)
• Rechenregeln:
  • (a + b) \mod n = ((a \mod n) + (b \mod n)) \mod n$(a + b) \mod n = ((a \mod n) + (b \mod n)) \mod n$
  • (a \cdot b) \mod n = ((a \mod n) \cdot (b \mod n)) \mod n$(a \cdot b) \mod n = ((a \mod n) \cdot (b \mod n)) \mod n$
  • (a \mod n) \mod n = a \mod n$(a \mod n) \mod n = a \mod n$
• Kongruenz:
  • a \equiv_n b$a \equiv_n b$: a$a$ und b$b$ haben bei Division durch n$n$ den gleichen Rest
  • Satz: a \equiv_n b \iff n | (a-b)$a \equiv_n b \iff n | (a-b)$
  • wenn a \equiv_n b$a \equiv_n b$ und c \equiv_n d$c \equiv_n d$, dann:
    • a + c \equiv_n b + d$a + c \equiv_n b + d$
    • a \cdot c \equiv_n b \cdot d$a \cdot c \equiv_n b \cdot d$
• Restklassen:
  • n\Z = \{..., -2n, -n, 0, n, 2n, ... \} = \{k \cdot n \; | \; k \in \Z \}$n\Z = \{..., -2n, -n, 0, n, 2n, ... \} = \{k \cdot n \; | \; k \in \Z \}$ ist eine Untergruppe von (\Z, +)$(\Z, +)$
  • Restklasse modulo n$n$: \forall a \in \Z: \overline a := a + n\Z$\forall a \in \Z: \overline a := a + n\Z$
  • Menge aller Restklassen: \Z_n := \{\overline 0, \overline 1, ..., \overline{n-1}\}$\Z_n := \{\overline 0, \overline 1, ..., \overline{n-1}\}$
    • \overline a +_n \overline b = \overline{a + b}$\overline a +_n \overline b = \overline{a + b}$
    • \overline a \cdot_n \overline b = \overline{a \cdot b}$\overline a \cdot_n \overline b = \overline{a \cdot b}$
  • kompletter Satz: a \equiv b \iff n | (a-b) \iff a + n\Z = b + n\Z \iff \overline a = \overline b$a \equiv b \iff n | (a-b) \iff a + n\Z = b + n\Z \iff \overline a = \overline b$
  • Restklassengrupe modulo n$n$: (\Z_n, +_n)$(\Z_n, +_n)$ ist eine kommutative Gruppe
  • Restklassenring modulo n$n$: (\Z_n, +_n, \cdot_n)$(\Z_n, +_n, \cdot_n)$ ist ein kommutativer Ring mit 1
  • Einheitengruppe: \Z^*_n = \{ \overline a \in \Z_n \; | \; ggT(a,n) = 1 \}$\Z^*_n = \{ \overline a \in \Z_n \; | \; ggT(a,n) = 1 \}$
    • wenn n$n$ prim, dann \Z^*_n = \Z_n \backslash \{ 0 \}$\Z^*_n = \Z_n \backslash \{ 0 \}$
    • (\Z_n, +_n, \cdot_n)$(\Z_n, +_n, \cdot_n)$ ist ein Körper genau dann, wenn n$n$ prim ist
• Eulerische Phi-Funktion:
  • \varphi(n) = |\{a \in \{1, ..., n\} \; | \; ggT(a,n) = 1|$\varphi(n) = |\{a \in \{1, ..., n\} \; | \; ggT(a,n) = 1|$
    • \varphi(p) = (p-1)$\varphi(p) = (p-1)$ für Primzahl p$p$
    • \varphi(pq) = (p-1)(q-1)$\varphi(pq) = (p-1)(q-1)$ für Primzahlen p$p$, q$q$
• der kleine Satz von Fermat:
  • wenn p$p$ prim, dann...
    • \forall a \in \Z \land ggT(a, p) = 1: a^{p-1} \equiv_p 1$\forall a \in \Z \land ggT(a, p) = 1: a^{p-1} \equiv_p 1$
    • \forall a \in \Z : a^p \equiv_p a$\forall a \in \Z : a^p \equiv_p a$
• EEA (Erweiterter Euklidischer Algorithmus), schamlos von DS kopiert:
  • Verfahren:
    • von oben nach unten: bestimme \lfloor b / a \rfloor$\lfloor b / a \rfloor$, trage Wert von a$a$ in unteren Zeile für b$b$ und den Rest b \mod a$b \mod a$ für a$a$ ein
      • wiederhole so lange, bis b \mod a = 0$b \mod a = 0$
    • von unten nach oben: setze \alpha = 1$\alpha = 1$ und \beta = 0$\beta = 0$, dann trage Wert von \alpha_{alt}$\alpha_{alt}$ in der oberen Zeile für \beta$\beta$ und \beta_{alt} - \lfloor b/a \rfloor_{current} \cdot \alpha_{alt}$\beta_{alt} - \lfloor b/a \rfloor_{current} \cdot \alpha_{alt}$ für \alpha$\alpha$ ein
      • wiederhole bis zur obersten Zeile
  • multiplikatives Inverse von a$a$ in \left< Z^*_n, \cdot_n, 1\right>$\left< Z^*_n, \cdot_n, 1\right>$ ist \alpha \mod n$\alpha \mod n$
  • Test auf ggT: ggT(a,b) = a \cdot \alpha + b \cdot \beta$ggT(a,b) = a \cdot \alpha + b \cdot \beta$

Lineare Codes

• Informationswort: x \in K^k$x \in K^k$ (oft K = \mathbb{F}_2 = \{0,1\}$K = \mathbb{F}_2 = \{0,1\}$)
  • z.B. x = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} \in \mathbb{F}_2^4$x = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} \in \mathbb{F}_2^4$
• Generatormatrix: G \in K^{n \times k}$G \in K^{n \times k}$
  • G = \begin{pmatrix} E_k \\ A \end{pmatrix}$G = \begin{pmatrix} E_k \\ A \end{pmatrix}$ (Einheitsmatrix oben, "Zusatzinfos" unten)
    • E_k$E_k$ hat k$k$ Zeilen
    • A$A$ hat n-k$n-k$ Zeilen
    • insgesamt k$k$ Spalten
  • z.B. Parity-Check-Code Generatormatrix G = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{pmatrix}$G = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{pmatrix}$
• Codewort (Generatormatrix mult. mit Informationswort): c := Gx$c := Gx$
  • \begin{pmatrix} c_1 \\ \vdots \\ c_n \end{pmatrix} = G \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \in K^n$\begin{pmatrix} c_1 \\ \vdots \\ c_n \end{pmatrix} = G \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \in K^n$
  • z.B. \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \in \mathbb{F}_2^5$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \in \mathbb{F}_2^5$
• Linearer Code: C := \{G \cdot x \; | \; x \in K^k\} = \text{Bild}(G) \leq K^n$C := \{G \cdot x \; | \; x \in K^k\} = \text{Bild}(G) \leq K^n$ (UVR)
  • \dim(C) = \text{rg}(G) = k$\dim(C) = \text{rg}(G) = k$ (d.h. Spalten von G$G$ sind Basis von C$C$)
• (n,k)$(n,k)$-Code:
  • \dim(C) = \text{rg}(G) = k$\dim(C) = \text{rg}(G) = k$
  • Informationsrate: \frac{k}{n}$\frac{k}{n}$
  • Redundanz: n-k$n-k$
• Kontrollmatrix: P = (-A \; \; E_{n-k})$P = (-A \; \; E_{n-k})$
  • \text{rg}(P) = n-k$\text{rg}(P) = n-k$
  • (!) P \cdot G = 0$P \cdot G = 0$
  • (!) P \cdot v = 0 \iff v \in C$P \cdot v = 0 \iff v \in C$ (bzw. C = \ker(P)$C = \ker(P)$)
  • -1 = 1$-1 = 1$ in \mathbb{F}_2$\mathbb{F}_2$
• REZEPT: Bestimmen eines empfangenen Informationswortes
  • gegeben: Funktion
    • z.B. (6,4)$(6,4)$-Code mit (x_1, x_2, x_3, x_4) \to (x_1, x_2, x_3, x_4, x_1 + x_2, x_3 + x_4) \in \mathbb{F}_2^6$(x_1, x_2, x_3, x_4) \to (x_1, x_2, x_3, x_4, x_1 + x_2, x_3 + x_4) \in \mathbb{F}_2^6$
  • bestimme Generatormatrix
    • z.B. G = \begin{pmatrix} E_4 \\ A \end{pmatrix}$G = \begin{pmatrix} E_4 \\ A \end{pmatrix}$ mit A = \begin{pmatrix}1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1\end{pmatrix}$A = \begin{pmatrix}1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1\end{pmatrix}$
  • bestimme, ob P \cdot c = 0$P \cdot c = 0$ (m.a.W. ob c \in C$c \in C$)
    • wenn nicht, dann müsste das Informationswort höchstwahrscheinlich noch einmal gesendet werden
  • löse LGS G \cdot x = c$G \cdot x = c$ und bestimme x$x$
• Dekodieren:
  • gesendet: c = (c_1, ... ,c_n)$c = (c_1, ... ,c_n)$
  • empfangen: c' = (c_1', ..., c_n')$c' = (c_1', ..., c_n')$
    • Fall 1: c' \in C$c' \in C$
      • nehme an, dass das richtige Codewort empfangen wurde (c' = c$c' = c$)
      • löse Gx = c'$Gx = c'$
    • Fall 2: c' \notin C$c' \notin C$
      • suche c'' \in C$c'' \in C$ mit möglichst wenig Abweichung zu c'$c'$
        • es gibt genau eins: nehme an, dass c'' = c$c'' = c$ (fehlerkorrigierend)
        • es gibt mehrere: Fehlermeldung (fehlererkennend)
• Hamming-Abstand:
  • für v = (v_1, ..., v_n) \in K^n$v = (v_1, ..., v_n) \in K^n$ ist w(v) = |\{i \in \{1, ..., n\} \; | \; v_i \neq 0\}|$w(v) = |\{i \in \{1, ..., n\} \; | \; v_i \neq 0\}|$ das Hamming-Gewicht von v$v$ (Anzahl aller Einträge ungleich 0)
    • z.B. w\begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = 4$w\begin{pmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = 4$
  • für v, v' \in K^n$v, v' \in K^n$ ist d(v, v') := w(v-v') = |\{i \in \{1, ..., n\} \; | \; v_i \neq v_i'\}|$d(v, v') := w(v-v') = |\{i \in \{1, ..., n\} \; | \; v_i \neq v_i'\}|$ der Hamming-Abstand von v$v$ und v'$v'$ (Anzahl aller Einträge, die in v$v$ und v'$v'$ nicht übereinstimmen)
    • z.B. d\left( \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \end{pmatrix} \right) = 3$d\left( \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \end{pmatrix} \right) = 3$
  • für eine Teilmenge C \subseteq K^n$C \subseteq K^n$ ist d(C) := \min\{d(c, c') \; | \; c,c' \in C \land c \neq c'\}$d(C) := \min\{d(c, c') \; | \; c,c' \in C \land c \neq c'\}$ der Hamming-Abstand von C$C$ (c$c$ und c'$c'$ unterscheiden sich an mindestens d(C)$d(C)$ Stellen)
    • falls |C| \leq 1$|C| \leq 1$, setze d(C) = n + 1$d(C) = n + 1$
    • für C \leq K^n$C \leq K^n$ ist d(C) = \min\{w(c) \; | \; c \in C \backslash \{0\} \}$d(C) = \min\{w(c) \; | \; c \in C \backslash \{0\} \}$
      • z.B. für C = (8,4)$C = (8,4)$-Wiederholungscode ist w_{\min}(c) = 2$w_{\min}(c) = 2$ für c = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$c = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$
  • Eigenschaften:
    • d(c,c') = 0 \iff c = c'$d(c,c') = 0 \iff c = c'$
    • d(c, c') = d(c', c)$d(c, c') = d(c', c)$
    • d(c, c'') \leq d(c,c') + d(c', c'')$d(c, c'') \leq d(c,c') + d(c', c'')$ (Dreiecksungleichung)
  • Satz:
    • falls d(C) = 2e+1$d(C) = 2e+1$ (ungerade), so ist C$C$ ein e$e$-fehlerkorrigierender Code
    • falls d(C) = 2e+2$d(C) = 2e+2$ (gerade), so ist C$C$ e$e$-fehlerkorrigierend und (e+1)$(e+1)$-fehlererkennend